Planning as Goal Recognition: Deriving Heuristics from Intention Models - Extended Version

Classical planning aims to find a sequence of actions, a plan, that maps a starting state into one of the goal states. If a trajectory appears to be leading to the goal, should we prioritise exploring it? Seminal work in goal recognition (GR) has defined GR in terms of a classical planning problem, adopting classical solvers and heuristics to recognise plans. We come full circle, and study the adoption and properties of GR-derived heuristics for seeking solutions to classical planning problems. We propose a new framework for assessing goal intention, which informs a new class of efficiently-computable heuristics. As a proof of concept, we derive two such heuristics, and show that they can already yield improvements for top-scoring classical planners. Our work provides foundational knowledge for understanding and deriving probabilistic intention-based heuristics for planning.

Count-based Novelty Exploration in Classical Planning

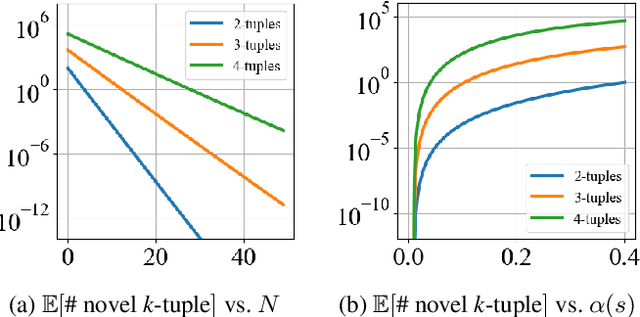
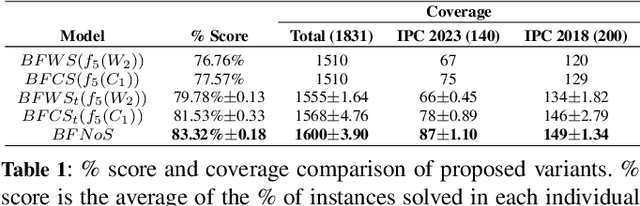
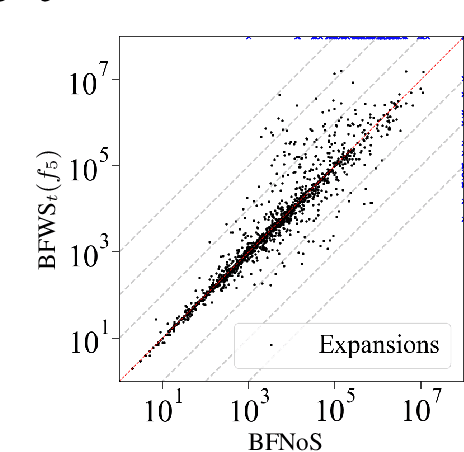
Count-based exploration methods are widely employed to improve the exploratory behavior of learning agents over sequential decision problems. Meanwhile, Novelty search has achieved success in Classical Planning through recording of the first, but not successive, occurrences of tuples. In order to structure the exploration, however, the number of tuples considered needs to grow exponentially as the search progresses. We propose a new novelty technique, classical count-based novelty, which aims to explore the state space with a constant number of tuples, by leveraging the frequency of each tuple's appearance in a search tree. We then justify the mechanisms through which lower tuple counts lead the search towards novel tuples. We also introduce algorithmic contributions in the form of a trimmed open list that maintains a constant size by pruning nodes with bad novelty values. These techniques are shown to complement existing novelty heuristics when integrated in a classical solver, achieving competitive results in challenging benchmarks from recent International Planning Competitions. Moreover, adapting our solver as the frontend planner in dual configurations that utilize both memory and time thresholds demonstrates a significant increase in instance coverage, surpassing current state-of-the-art solvers.