Gert Smolka
A Complete and Recursive Feature Theory
Jun 17, 1994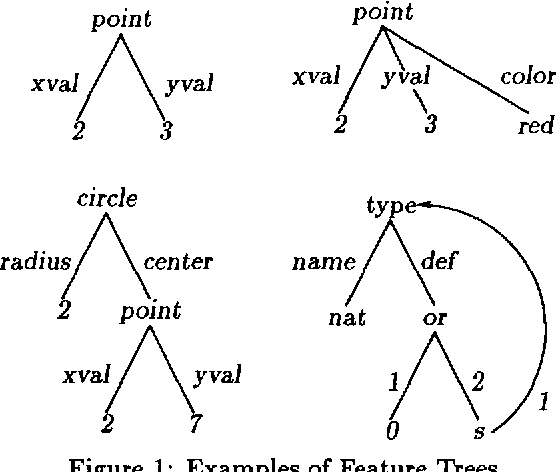
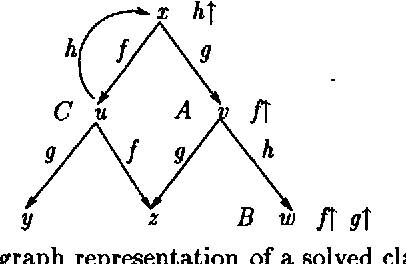
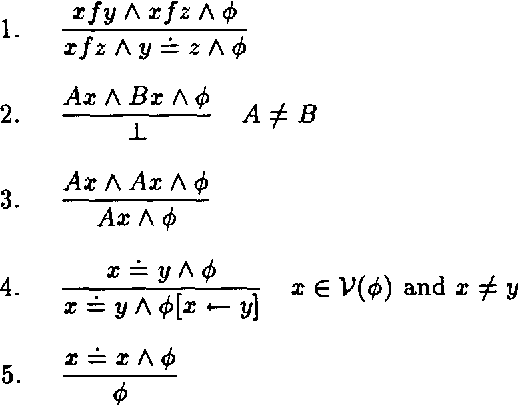
Abstract:Various feature descriptions are being employed in logic programming languages and constrained-based grammar formalisms. The common notational primitive of these descriptions are functional attributes called features. The descriptions considered in this paper are the possibly quantified first-order formulae obtained from a signature of binary and unary predicates called features and sorts, respectively. We establish a first-order theory FT by means of three axiom schemes, show its completeness, and construct three elementarily equivalent models. One of the models consists of so-called feature graphs, a data structure common in computational linguistics. The other two models consist of so-called feature trees, a record-like data structure generalizing the trees corresponding to first-order terms. Our completeness proof exhibits a terminating simplification system deciding validity and satisfiability of possibly quantified feature descriptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge