cuFINUFFT: a load-balanced GPU library for general-purpose nonuniform FFTs

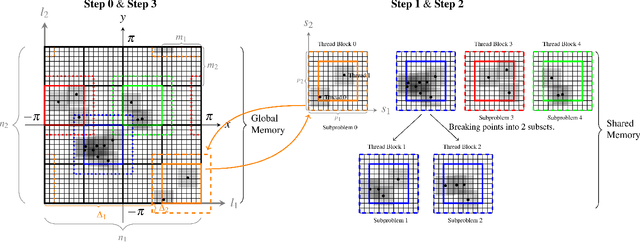
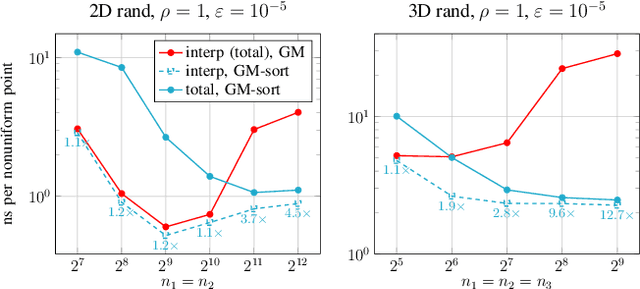
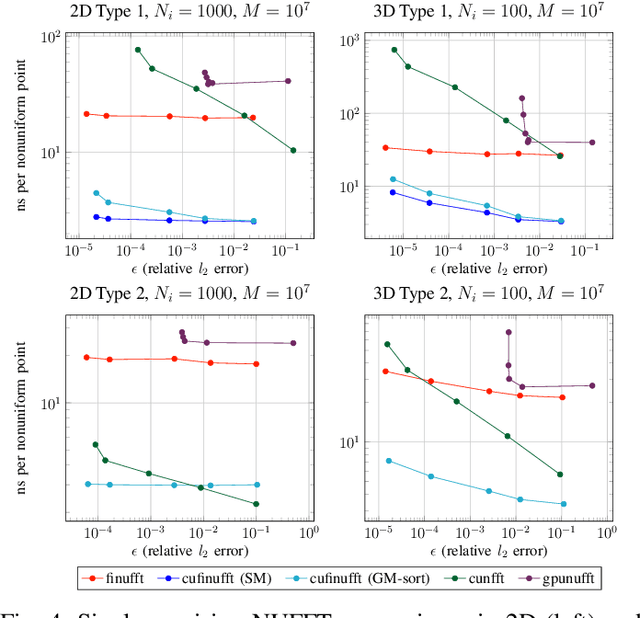
Nonuniform fast Fourier transforms dominate the computational cost in many applications including image reconstruction and signal processing. We thus present a general-purpose GPU-based CUDA library for type 1 (nonuniform to uniform) and type 2 (uniform to nonuniform) transforms in dimensions 2 and 3, in single or double precision. It achieves high performance for a given user-requested accuracy, regardless of the distribution of nonuniform points, via cache-aware point reordering, and load-balanced blocked spreading in shared memory. At low accuracies, this gives on-GPU throughputs around $10^9$ nonuniform points per second, and (even including host-device transfer) is typically 4-10$\times$ faster than the latest parallel CPU code FINUFFT (at 28 threads). It is competitive with two established GPU codes, being up to 90$\times$ faster at high accuracy and/or type 1 clustered point distributions. Finally we demonstrate a 6-18$\times$ speedup versus CPU in an X-ray diffraction 3D iterative reconstruction task at $10^{-12}$ accuracy, observing excellent multi-GPU weak scaling up to one rank per GPU.

Improved Time Warp Edit Distance -- A Parallel Dynamic Program in Linear Memory

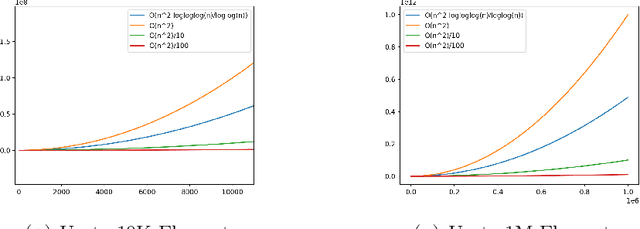
Edit Distance is a classic family of dynamic programming problems, among which Time Warp Edit Distance refines the problem with the notion of a metric and temporal elasticity. A novel Improved Time Warp Edit Distance algorithm that is both massively parallelizable and requiring only linear storage is presented. This method uses the procession of a three diagonal band to cover the original dynamic program space. Every element of the diagonal update can be computed in parallel. The core method is a feature of the TWED Longest Common Subsequence data dependence and is applicable to dynamic programs that share similar band subproblem structure. The algorithm has been implemented as a CUDA C library with Python bindings. Speedups for challenging problems are phenomenal.