Identifying Systems with Symmetries using Equivariant Autoregressive Reservoir Computers

The investigation reported in this document focuses on identifying systems with symmetries using equivariant autoregressive reservoir computers. General results in structured matrix approximation theory are presented, exploring a two-fold approach. Firstly, a comprehensive examination of generic symmetry-preserving nonlinear time delay embedding is conducted. This involves analyzing time series data sampled from an equivariant system under study. Secondly, sparse least-squares methods are applied to discern approximate representations of the output coupling matrices. These matrices play a pivotal role in determining the nonlinear autoregressive representation of an equivariant system. The structural characteristics of these matrices are dictated by the set of symmetries inherent in the system. The document outlines prototypical algorithms derived from the described techniques, offering insight into their practical applications. Emphasis is placed on their effectiveness in the identification and predictive simulation of equivariant nonlinear systems, regardless of whether such systems exhibit chaotic behavior.

Dynamic financial processes identification using sparse regressive reservoir computers

In this document, we present key findings in structured matrix approximation theory, with applications to the regressive representation of dynamic financial processes. Initially, we explore a comprehensive approach involving generic nonlinear time delay embedding for time series data extracted from a financial or economic system under examination. Subsequently, we employ sparse least-squares and structured matrix approximation methods to discern approximate representations of the output coupling matrices. These representations play a pivotal role in establishing the regressive models corresponding to the recursive structures inherent in a given financial system. The document further introduces prototypical algorithms that leverage the aforementioned techniques. These algorithms are demonstrated through applications in approximate identification and predictive simulation of dynamic financial and economic processes, encompassing scenarios that may or may not exhibit chaotic behavior.

A Subspace Method for Time Series Anomaly Detection in Cyber-Physical Systems

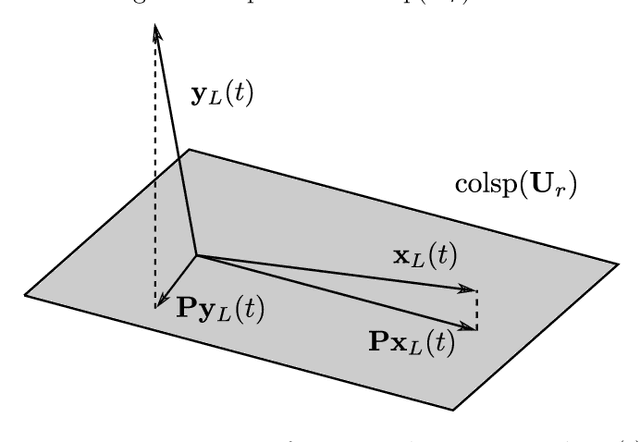
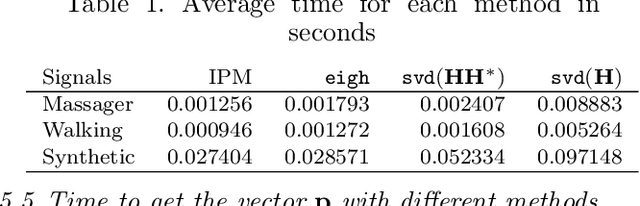
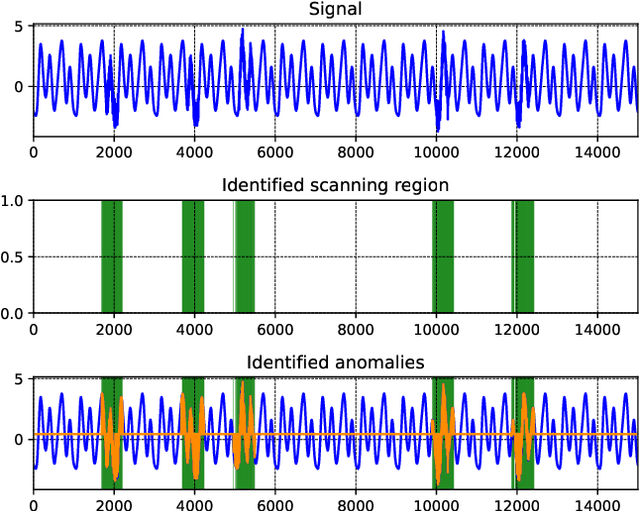
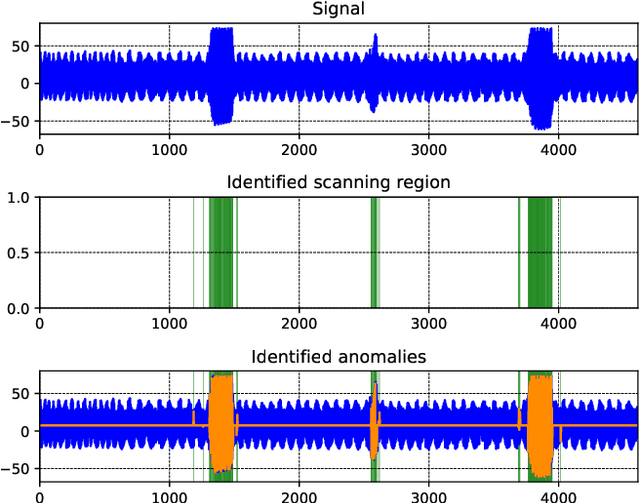
Time series anomaly detection is an important process for system monitoring and model switching, among other applications in cyber-physical systems. In this document, we present a fast subspace method for time series anomaly detection, with a relatively low computational cost, that has been designed for anomaly detection in real sensor signals corresponding to dynamical systems. We also present some general results corresponding to the theoretical foundations of our method, together with a prototypical algorithm to for time series anomaly detection. Some numerical examples corresponding to applications of the prototypical algorithm are presented, and some computational tools based on the theory and algorithms presented in this paper, are provided.

Computing Semilinear Sparse Models for Approximately Eventually Periodic Signals

Some elements of the theory and algorithmics corresponding to the computation of semilinear sparse models for discrete-time signals are presented. In this study, we will focus on approximately eventually periodic discrete-time signals, that is, signals that can exhibit an aperiodic behavior for an initial amount of time, and then become approximately periodic afterwards. The semilinear models considered in this study are obtained by combining sparse representation methods, linear autoregressive models and GRU neural network models, initially fitting each block model independently using some reference data corresponding to some signal under consideration, and then fitting some mixing parameters that are used to obtain a signal model consisting of a linear combination of the previously fitted blocks using the aforementioned reference data, computing sparse representations of some of the matrix parameters of the resulting model along the process. Some prototypical computational implementations are presented as well.