Fuzzy Clustering by Hyperbolic Smoothing

We propose a novel method for building fuzzy clusters of large data sets, using a smoothing numerical approach. The usual sum-of-squares criterion is relaxed so the search for good fuzzy partitions is made on a continuous space, rather than a combinatorial space as in classical methods \cite{Hartigan}. The smoothing allows a conversion from a strongly non-differentiable problem into differentiable subproblems of optimization without constraints of low dimension, by using a differentiable function of infinite class. For the implementation of the algorithm we used the statistical software $R$ and the results obtained were compared to the traditional fuzzy $C$--means method, proposed by Bezdek.

A Subspace Method for Time Series Anomaly Detection in Cyber-Physical Systems

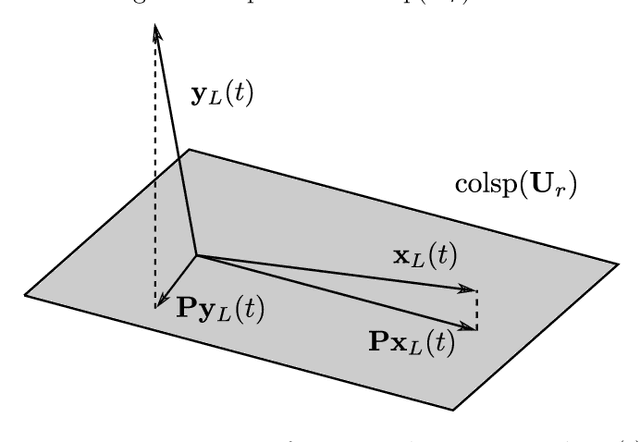
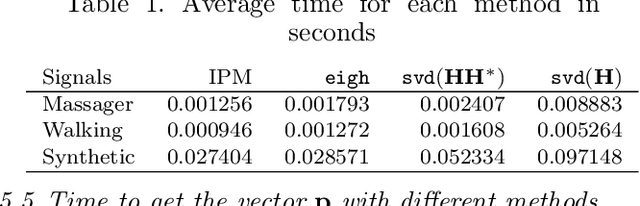
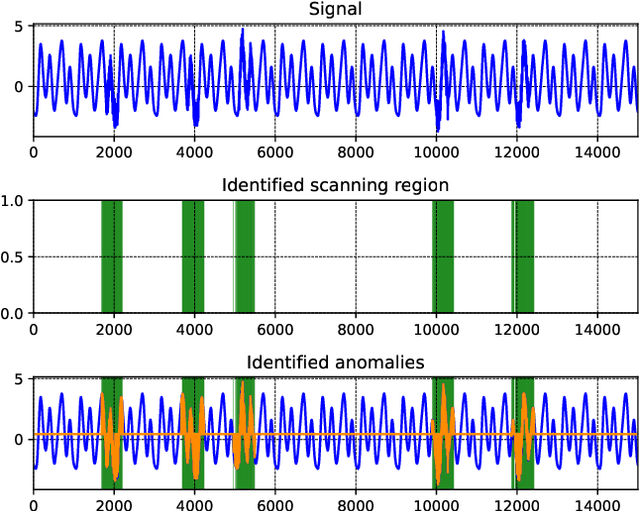
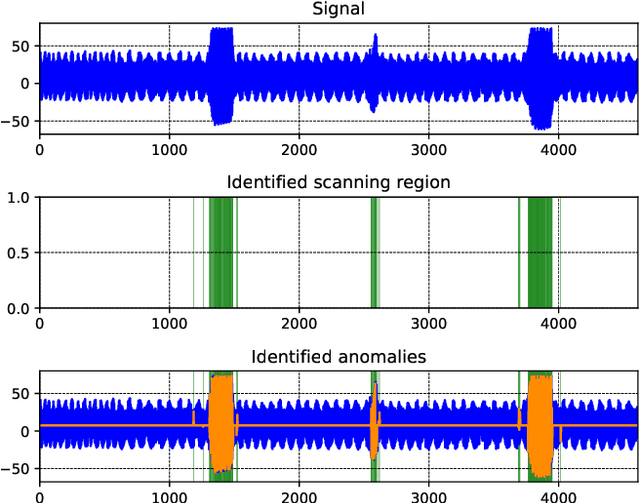
Time series anomaly detection is an important process for system monitoring and model switching, among other applications in cyber-physical systems. In this document, we present a fast subspace method for time series anomaly detection, with a relatively low computational cost, that has been designed for anomaly detection in real sensor signals corresponding to dynamical systems. We also present some general results corresponding to the theoretical foundations of our method, together with a prototypical algorithm to for time series anomaly detection. Some numerical examples corresponding to applications of the prototypical algorithm are presented, and some computational tools based on the theory and algorithms presented in this paper, are provided.