Heuristic Search for Rank Aggregation with Application to Label Ranking

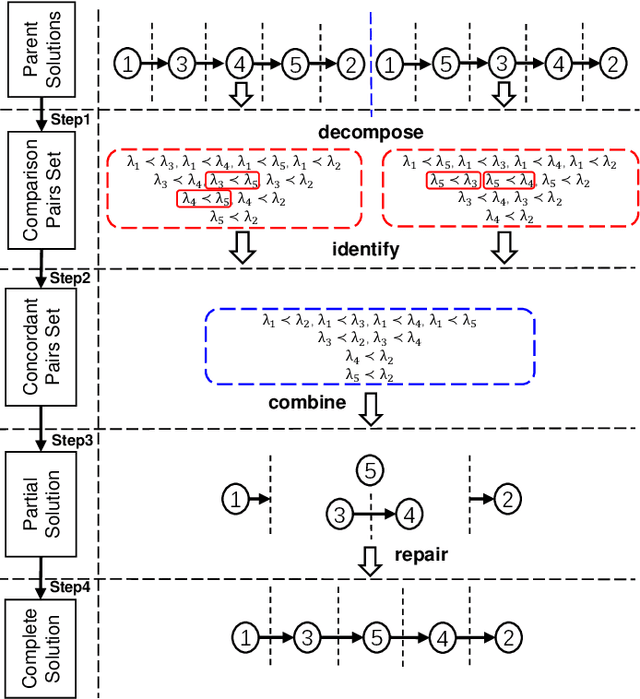
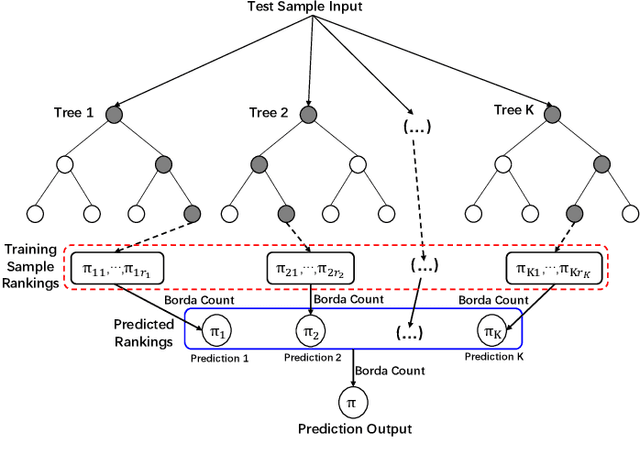
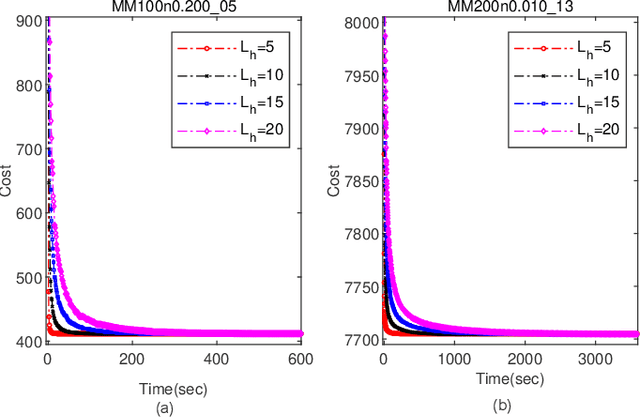
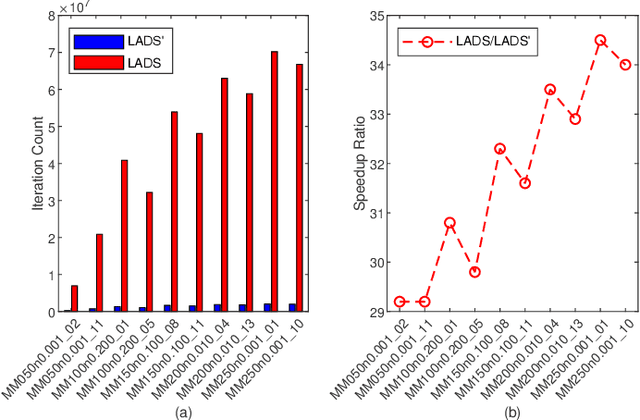
Rank aggregation aims to combine the preference rankings of a number of alternatives from different voters into a single consensus ranking. As a useful model for a variety of practical applications, however, it is a computationally challenging problem. In this paper, we propose an effective hybrid evolutionary ranking algorithm to solve the rank aggregation problem with both complete and partial rankings. The algorithm features a semantic crossover based on concordant pairs and a late acceptance local search reinforced by an efficient incremental evaluation technique. Experiments are conducted to assess the algorithm, indicating a highly competitive performance on benchmark instances compared with state-of-the-art algorithms. To demonstrate its practical usefulness, the algorithm is applied to label ranking, which is an important machine learning task.

Exploiting Local Optimality in Metaheuristic Search

A variety of strategies have been proposed for overcoming local optimality in metaheuristic search. This paper examines characteristics of moves that can be exploited to make good decisions about steps that lead away from a local optimum and then lead toward a new local optimum. We introduce strategies to identify and take advantage of useful features of solution history with an adaptive memory metaheuristic, to provide rules for selecting moves that offer promise for discovering improved local optima. Our approach uses a new type of adaptive memory based on a construction called exponential extrapolation. The memory operates by means of threshold inequalities that ensure selected moves will not lead to a specified number of most recently encountered local optima. Associated thresholds are embodied in choice rule strategies that further exploit the exponential extrapolation concept. Together these produce a threshold based Alternating Ascent (AA) algorithm that opens a variety of research possibilities for exploration.

Bi-objective Optimization of Biclustering with Binary Data

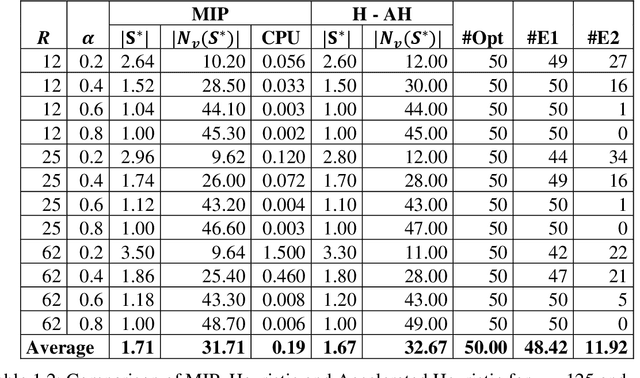
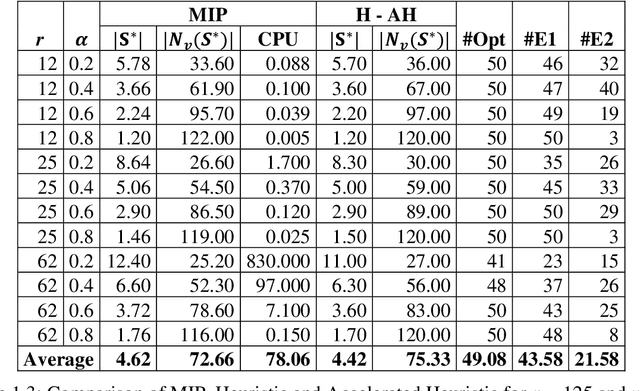
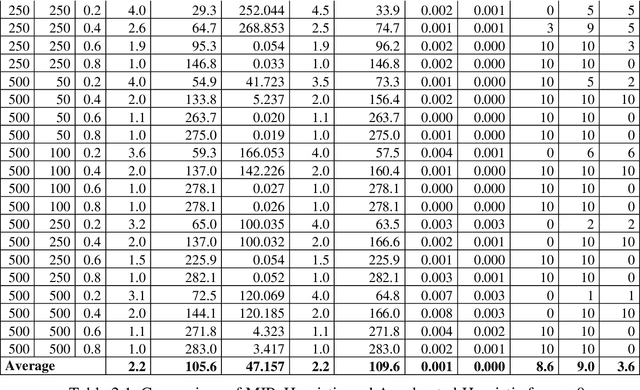
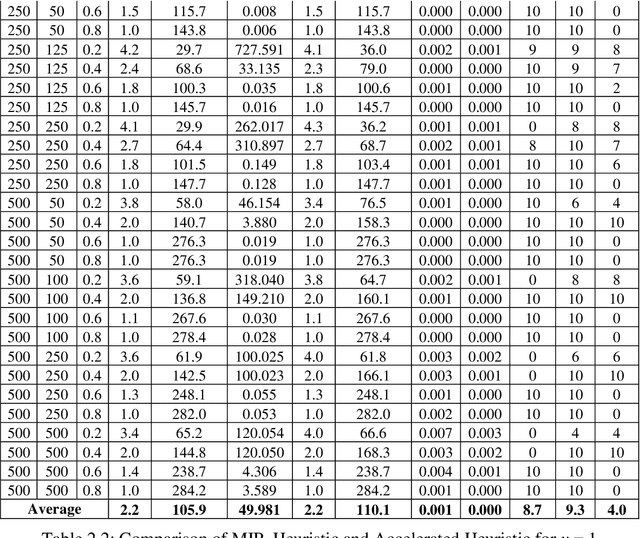
Clustering consists of partitioning data objects into subsets called clusters according to some similarity criteria. This paper addresses a generalization called quasi-clustering that allows overlapping of clusters, and which we link to biclustering. Biclustering simultaneously groups the objects and features so that a specific group of objects has a special group of features. In recent years, biclustering has received a lot of attention in several practical applications. In this paper we consider a bi-objective optimization of biclustering problem with binary data. First we present an integer programing formulations for the bi-objective optimization biclustering. Next we propose a constructive heuristic based on the set intersection operation and its efficient implementation for solving a series of mono-objective problems used inside the Epsilon-constraint method (obtained by keeping only one objective function and the other objective function is integrated into constraints). Finally, our experimental results show that using CPLEX solver as an exact algorithm for finding an optimal solution drastically increases the computational cost for large instances, while our proposed heuristic provides very good results and significantly reduces the computational expense.

Memetic search for identifying critical nodes in sparse graphs

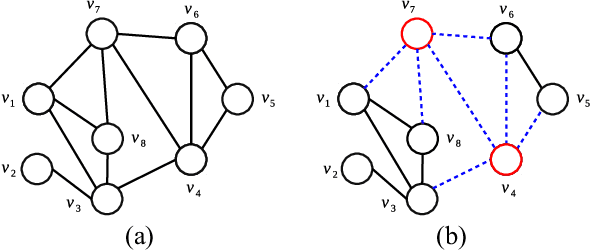
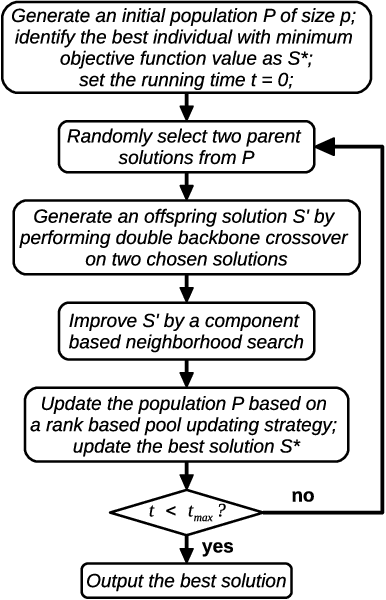
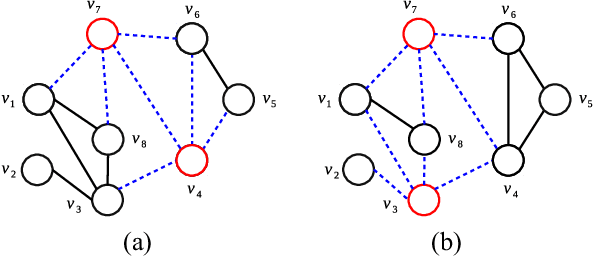
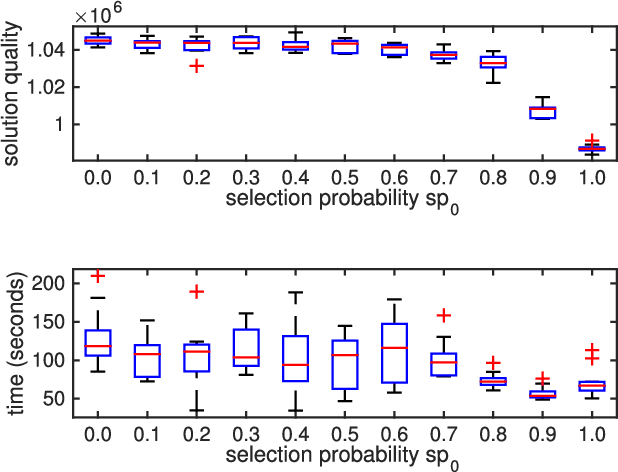
Critical node problems involve identifying a subset of critical nodes from an undirected graph whose removal results in optimizing a pre-defined measure over the residual graph. As useful models for a variety of practical applications, these problems are computational challenging. In this paper, we study the classic critical node problem (CNP) and introduce an effective memetic algorithm for solving CNP. The proposed algorithm combines a double backbone-based crossover operator (to generate promising offspring solutions), a component-based neighborhood search procedure (to find high-quality local optima) and a rank-based pool updating strategy (to guarantee a healthy population). Specially, the component-based neighborhood search integrates two key techniques, i.e., two-phase node exchange strategy and node weighting scheme. The double backbone-based crossover extends the idea of general backbone-based crossovers. Extensive evaluations on 42 synthetic and real-world benchmark instances show that the proposed algorithm discovers 21 new upper bounds and matches 18 previous best-known upper bounds. We also demonstrate the relevance of our algorithm for effectively solving a variant of the classic CNP, called the cardinality-constrained critical node problem. Finally, we investigate the usefulness of each key algorithmic component.

Quadratic Unconstrained Binary Optimization Problem Preprocessing: Theory and Empirical Analysis

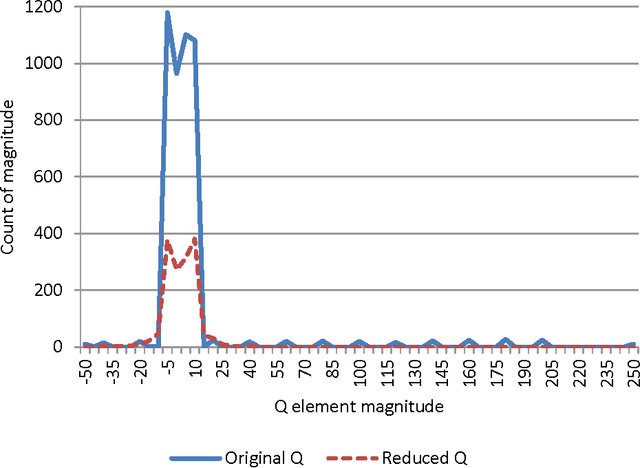
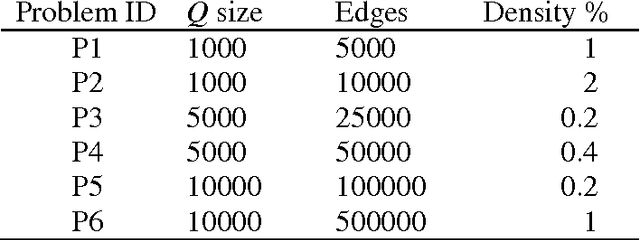
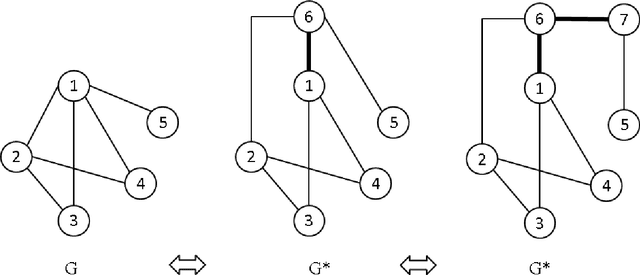
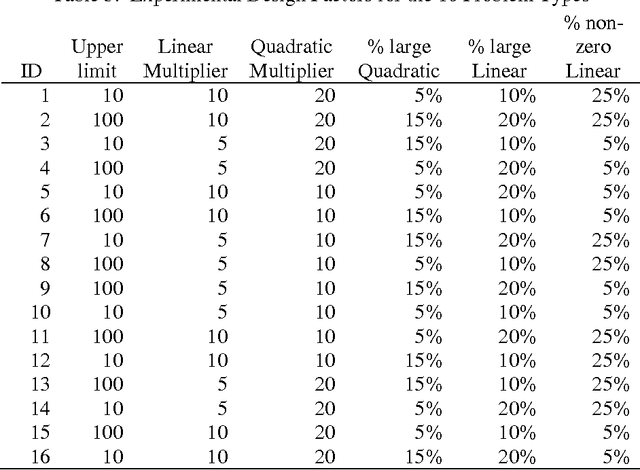
The Quadratic Unconstrained Binary Optimization problem (QUBO) has become a unifying model for representing a wide range of combinatorial optimization problems, and for linking a variety of disciplines that face these problems. A new class of quantum annealing computer that maps QUBO onto a physical qubit network structure with specific size and edge density restrictions is generating a growing interest in ways to transform the underlying QUBO structure into an equivalent graph having fewer nodes and edges. In this paper we present rules for reducing the size of the QUBO matrix by identifying variables whose value at optimality can be predetermined. We verify that the reductions improve both solution quality and time to solution and, in the case of metaheuristic methods where optimal solutions cannot be guaranteed, the quality of solutions obtained within reasonable time limits. We discuss the general QUBO structural characteristics that can take advantage of these reduction techniques and perform careful experimental design and analysis to identify and quantify the specific characteristics most affecting reduction. The rules make it possible to dramatically improve solution times on a new set of problems using both the exact Cplex solver and a tabu search metaheuristic.

Logical and Inequality Implications for Reducing the Size and Complexity of Quadratic Unconstrained Binary Optimization Problems

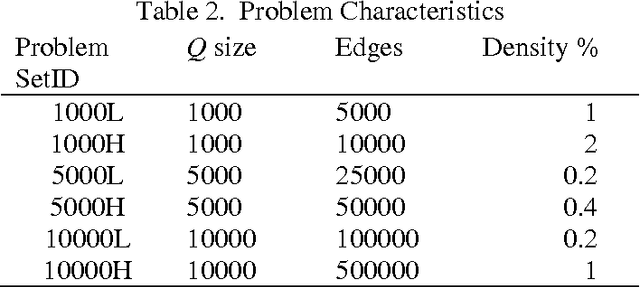
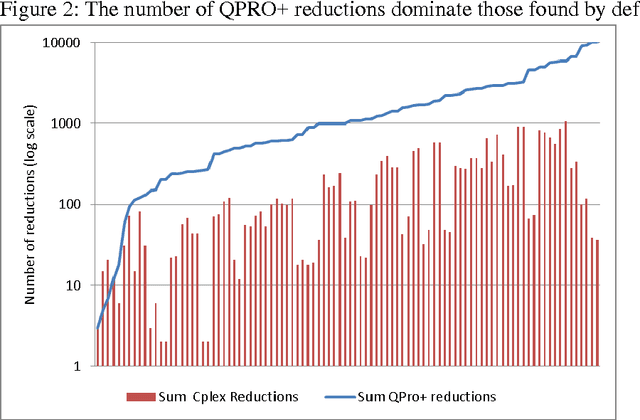
The quadratic unconstrained binary optimization (QUBO) problem arises in diverse optimization applications ranging from Ising spin problems to classical problems in graph theory and binary discrete optimization. The use of preprocessing to transform the graph representing the QUBO problem into a smaller equivalent graph is important for improving solution quality and time for both exact and metaheuristic algorithms and is a step towards mapping large scale QUBO to hardware graphs used in quantum annealing computers. In an earlier paper (Lewis and Glover, 2016) a set of rules was introduced that achieved significant QUBO reductions as verified through computational testing. Here this work is extended with additional rules that provide further reductions that succeed in exactly solving 10% of the benchmark QUBO problems. An algorithm and associated data structures to efficiently implement the entire set of rules is detailed and computational experiments are reported that demonstrate their efficacy.

A History of Metaheuristics

This chapter describes the history of metaheuristics in five distinct periods, starting long before the first use of the term and ending a long time in the future.

Diversification-Based Learning in Computing and Optimization

Diversification-Based Learning (DBL) derives from a collection of principles and methods introduced in the field of metaheuristics that have broad applications in computing and optimization. We show that the DBL framework goes significantly beyond that of the more recent Opposition-based learning (OBL) framework introduced in Tizhoosh (2005), which has become the focus of numerous research initiatives in machine learning and metaheuristic optimization. We unify and extend earlier proposals in metaheuristic search (Glover, 1997, Glover and Laguna, 1997) to give a collection of approaches that are more flexible and comprehensive than OBL for creating intensification and diversification strategies in metaheuristic search. We also describe potential applications of DBL to various subfields of machine learning and optimization.

Diversification Methods for Zero-One Optimization

We introduce new diversification methods for zero-one optimization that significantly extend strategies previously introduced in the setting of metaheuristic search. Our methods incorporate easily implemented strategies for partitioning assignments of values to variables, accompanied by processes called augmentation and shifting which create greater flexibility and generality. We then show how the resulting collection of diversified solutions can be further diversified by means of permutation mappings, which equally can be used to generate diversified collections of permutations for applications such as scheduling and routing. These methods can be applied to non-binary vectors by the use of binarization procedures and by Diversification-Based Learning (DBL) procedures which also provide connections to applications in clustering and machine learning. Detailed pseudocode and numerical illustrations are provided to show the operation of our methods and the collections of solutions they create.

Integrating tabu search and VLSN search to develop enhanced algorithms: A case study using bipartite boolean quadratic programs

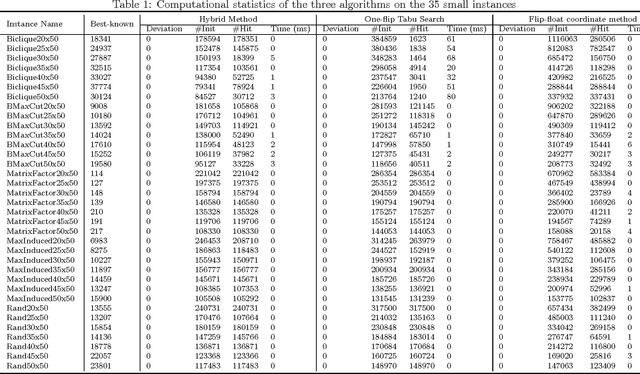
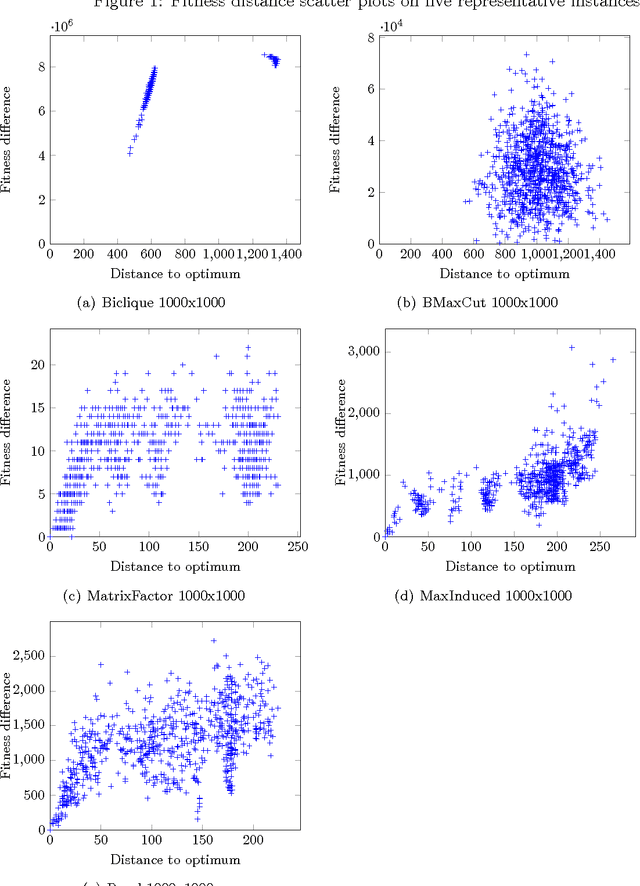
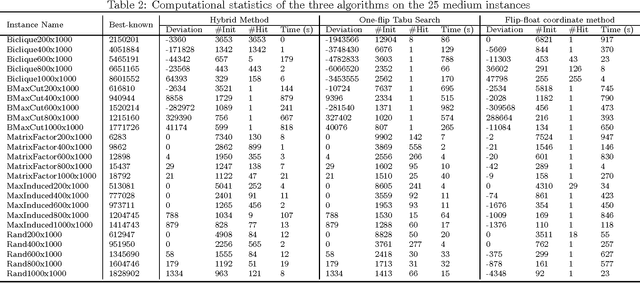
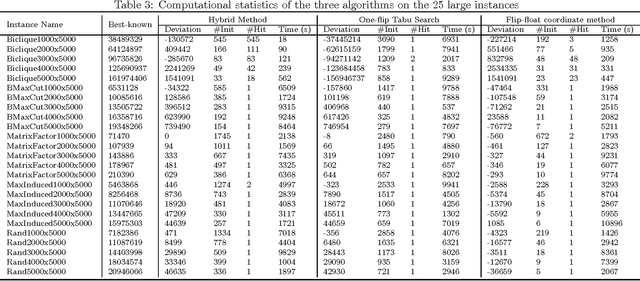
The bipartite boolean quadratic programming problem (BBQP) is a generalization of the well studied boolean quadratic programming problem. The model has a variety of real life applications; however, empirical studies of the model are not available in the literature, except in a few isolated instances. In this paper, we develop efficient heuristic algorithms based on tabu search, very large scale neighborhood (VLSN) search, and a hybrid algorithm that integrates the two. The computational study establishes that effective integration of simple tabu search with VLSN search results in superior outcomes, and suggests the value of such an integration in other settings. Complexity analysis and implementation details are provided along with conclusions drawn from experimental analysis. In addition, we obtain solutions better than the best previously known for almost all medium and large size benchmark instances.