Francisco J. Valverde-Albacete
Assessing Information Transmission in Data Transformations with the Channel Multivariate Entropy Triangle
Oct 10, 2018

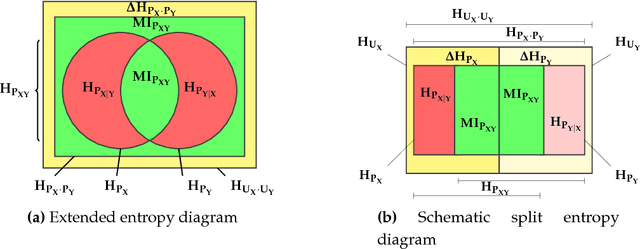

Abstract:Data transformation, e.g. feature transformation and selection, is an integral part of any machine learning procedure. In this paper we introduce an information-theoretic model and tools to assess the quality of data transformations in machine learning tasks. In an unsupervised fashion, we analyze the transfer of information of the transformation of a discrete, multivariate source of information X into a discrete, multivariate sink of information Y related by a distribution PXY . The first contribution is a decomposition of the maximal potential entropy of (X, Y) that we call a balance equation, into its a) non-transferable, b) transferable but not transferred and c) transferred parts. Such balance equations can be represented in (de Finetti) entropy diagrams, our second set of contributions. The most important of these, the aggregate Channel Multivariate Entropy Triangle is a visual exploratory tool to assess the effectiveness of multivariate data transformations in transferring information from input to output variables. We also show how these decomposition and balance equation also apply to the entropies of X and Y respectively and generate entropy triangles for them. As an example, we present the application of these tools to the assessment of information transfer efficiency for PCA and ICA as unsupervised feature transformation and selection procedures in supervised classification tasks.
* 21 pages, 7 figures and 1 table
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge