A General Framework for Partial to Full Image Registration

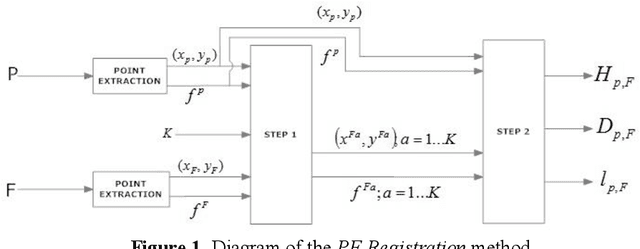
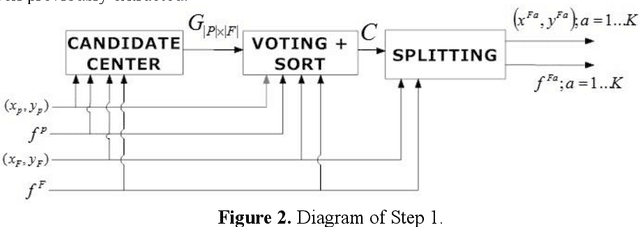
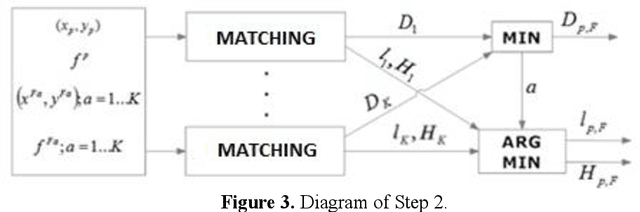
Image registration is a research field in which images must be compared and aligned independently of the point of view or camera characteristics. In some applications (such as forensic biometrics, satellite photography or outdoor scene identification) classical image registration systems fail due to one of the images compared represents a tiny piece of the other image. For instance, in forensics palmprint recognition, it is usual to find only a small piece of the palmprint, but in the database, the whole palmprint has been enrolled. The main reason of the poor behaviour of classical image registration methods is the gap between the amounts of salient points of both images, which is related to the number of points to be considered as outliers. Usually, the difficulty of finding a good match increases when the image that represents the tiny part of the scene has been drastically rotated. Again, in the case of palmprint forensics, it is difficult to decide a priori the orientation of the found tiny palmprint image. We present a rotation invariant registration method that explicitly considers that the image to be matched is a small piece of a larger image. We have experimentally validated our method in two different scenarios; palmprint identification and outdoor image registration.

Function-Described Graphs for Structural Pattern Recognition

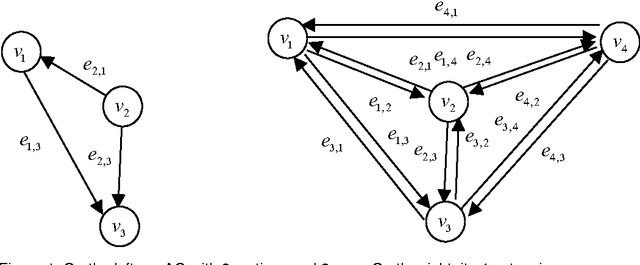
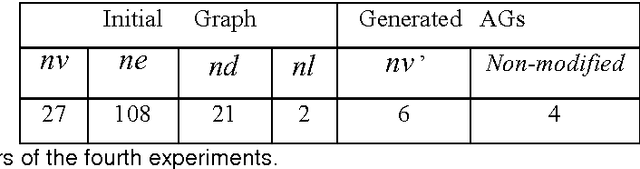
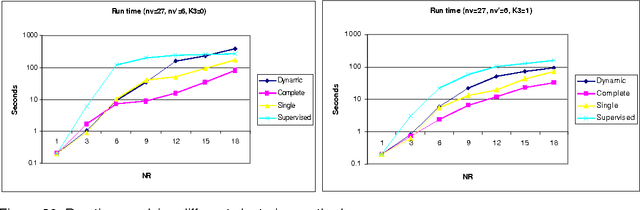
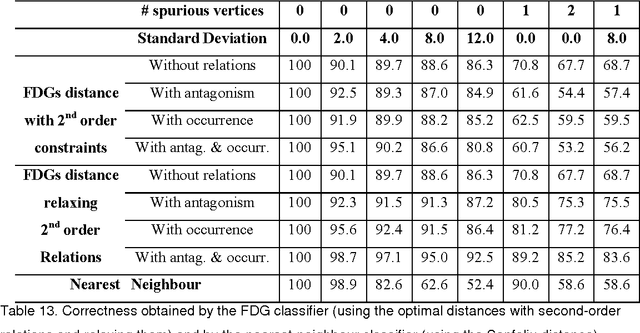
We present in this article the model Function-described graph (FDG), which is a type of compact representation of a set of attributed graphs (AGs) that borrow from Random Graphs the capability of probabilistic modelling of structural and attribute information. We define the FDGs, their features and two distance measures between AGs (unclassified patterns) and FDGs (models or classes) and we also explain an efficient matching algorithm. Two applications of FDGs are presented: in the former, FDGs are used for modelling and matching 3D-objects described by multiple views, whereas in the latter, they are used for representing and recognising human faces, described also by several views.

On the Relation Between the Common Labelling and the Median Graph

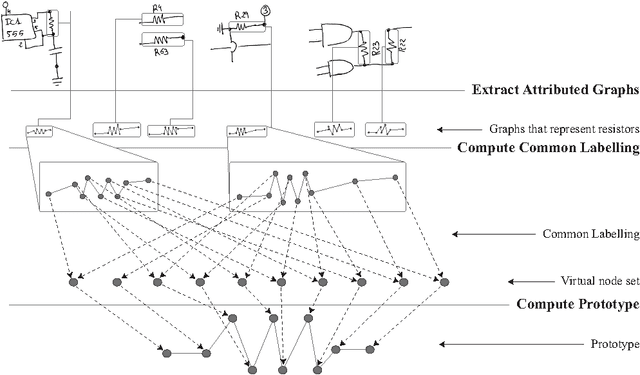
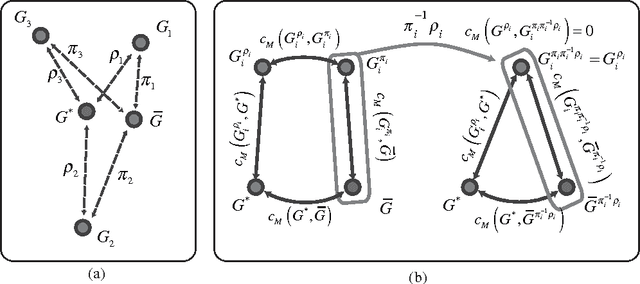
In structural pattern recognition, given a set of graphs, the computation of a Generalized Median Graph is a well known problem. Some methods approach the problem by assuming a relation between the Generalized Median Graph and the Common Labelling problem. However, this relation has still not been formally proved. In this paper, we analyse such relation between both problems. The main result proves that the cost of the common labelling upper-bounds the cost of the median with respect to the given set. In addition, we show that the two problems are equivalent in some cases.