A score-based operator Newton method for measure transport

Transportation of probability measures underlies many core tasks in statistics and machine learning, from variational inference to generative modeling. A typical goal is to represent a target probability measure of interest as the push-forward of a tractable source measure through a learned map. We present a new construction of such a transport map, given the ability to evaluate the score of the target distribution. Specifically, we characterize the map as a zero of an infinite-dimensional score-residual operator and derive a Newton-type method for iteratively constructing such a zero. We prove convergence of these iterations by invoking classical elliptic regularity theory for partial differential equations (PDE) and show that this construction enjoys rapid convergence, under smoothness assumptions on the target score. A key element of our approach is a generalization of the elementary Newton method to infinite-dimensional operators, other forms of which have appeared in nonlinear PDE and in dynamical systems. Our Newton construction, while developed in a functional setting, also suggests new iterative algorithms for approximating transport maps.

Evaluating Machine Learning Models for the Fast Identification of Contingency Cases

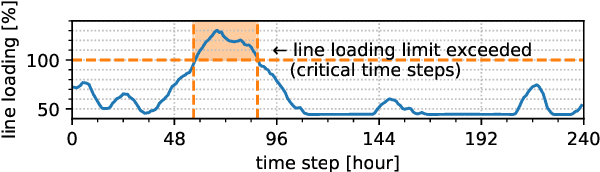
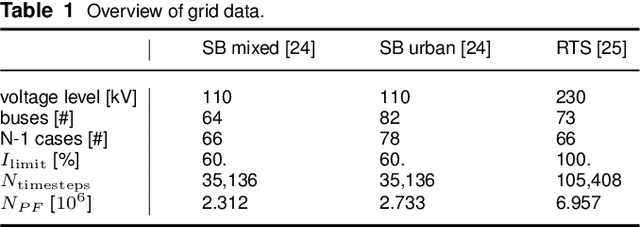
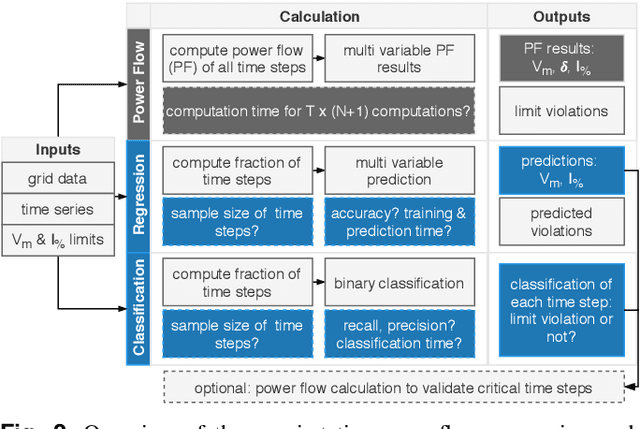
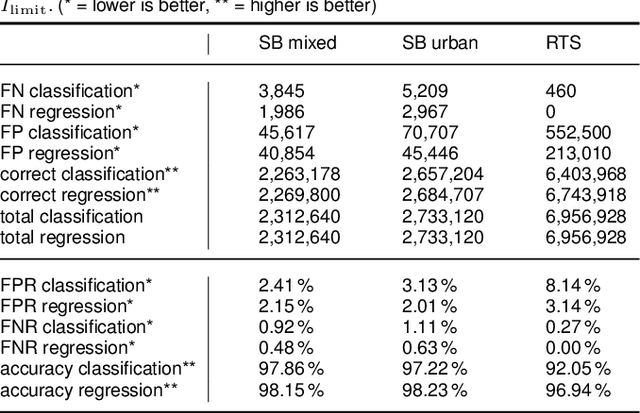
Fast approximations of power flow results are beneficial in power system planning and live operation. In planning, millions of power flow calculations are necessary if multiple years, different control strategies or contingency policies are to be considered. In live operation, grid operators must assess if grid states comply with contingency requirements in a short time. In this paper, we compare regression and classification methods to either predict multi-variable results, e.g. bus voltage magnitudes and line loadings, or binary classifications of time steps to identify critical loading situations. We test the methods on three realistic power systems based on time series in 15 min and 5 min resolution of one year. We compare different machine learning models, such as multilayer perceptrons (MLPs), decision trees, k-nearest neighbours, gradient boosting, and evaluate the required training time and prediction times as well as the prediction errors. We additionally determine the amount of training data needed for each method and show results, including the approximation of untrained curtailment of generation. Regarding the compared methods, we identified the MLPs as most suitable for the task. The MLP-based models can predict critical situations with an accuracy of 97-98 % and a very low number of false negative predictions of 0.0-0.64 %.