Unreasonable Effectivness of Deep Learning

We show how well known rules of back propagation arise from a weighted combination of finite automata. By redefining a finite automata as a predictor we combine the set of all $k$-state finite automata using a weighted majority algorithm. This aggregated prediction algorithm can be simplified using symmetry, and we prove the equivalence of an algorithm that does this. We demonstrate that this algorithm is equivalent to a form of a back propagation acting in a completely connected $k$-node neural network. Thus the use of the weighted majority algorithm allows a bound on the general performance of deep learning approaches to prediction via known results from online statistics. The presented framework opens more detailed questions about network topology; it is a bridge to the well studied techniques of semigroup theory and applying these techniques to answer what specific network topologies are capable of predicting. This informs both the design of artificial networks and the exploration of neuroscience models.

Prediction with Restricted Resources and Finite Automata

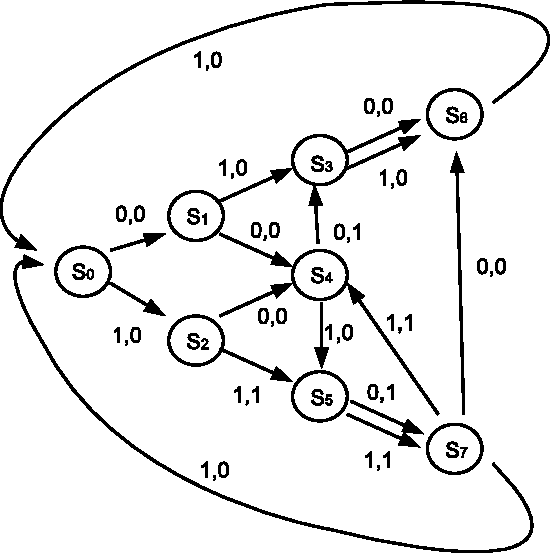
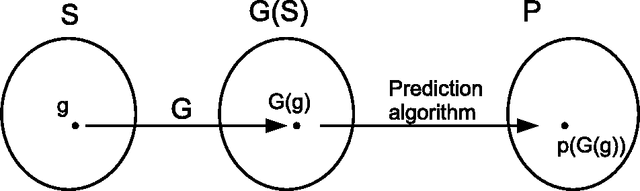
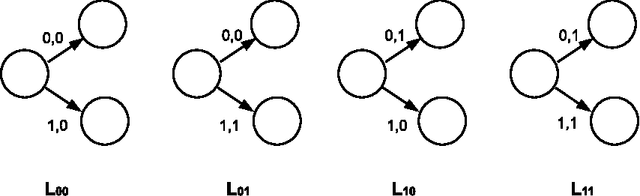
We obtain an index of the complexity of a random sequence by allowing the role of the measure in classical probability theory to be played by a function we call the generating mechanism. Typically, this generating mechanism will be a finite automata. We generate a set of biased sequences by applying a finite state automata with a specified number, $m$, of states to the set of all binary sequences. Thus we can index the complexity of our random sequence by the number of states of the automata. We detail optimal algorithms to predict sequences generated in this way.