Prediction with Restricted Resources and Finite Automata
Paper and Code
Dec 10, 2008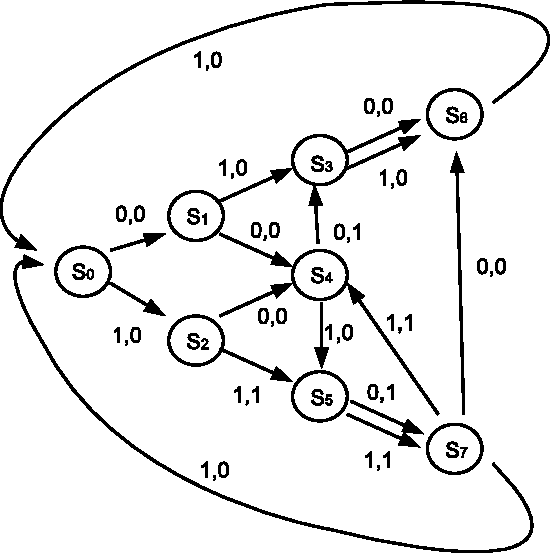
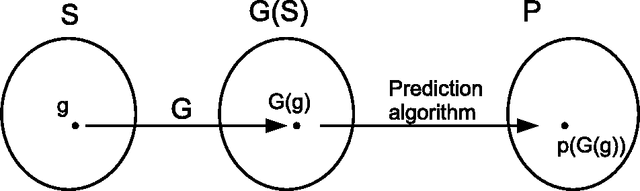
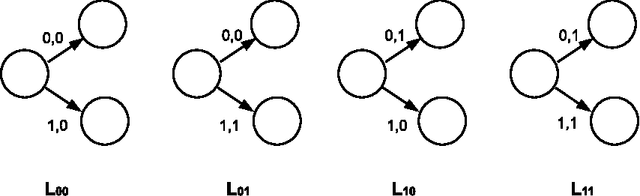
We obtain an index of the complexity of a random sequence by allowing the role of the measure in classical probability theory to be played by a function we call the generating mechanism. Typically, this generating mechanism will be a finite automata. We generate a set of biased sequences by applying a finite state automata with a specified number, $m$, of states to the set of all binary sequences. Thus we can index the complexity of our random sequence by the number of states of the automata. We detail optimal algorithms to predict sequences generated in this way.
* 13 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge