Filip Sadlo
Topological Machine Learning with Persistence Indicator Functions
Jul 31, 2019
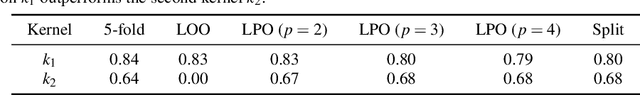
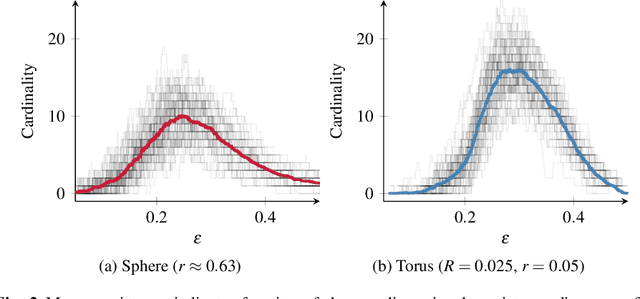
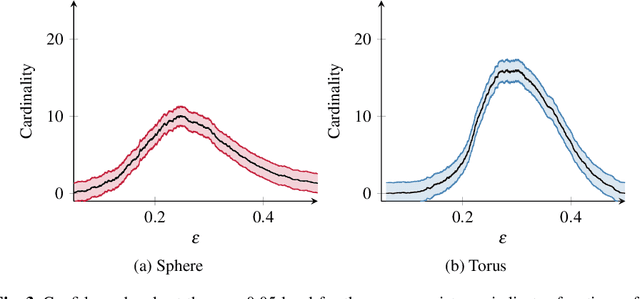
Abstract:Techniques from computational topology, in particular persistent homology, are becoming increasingly relevant for data analysis. Their stable metrics permit the use of many distance-based data analysis methods, such as multidimensional scaling, while providing a firm theoretical ground. Many modern machine learning algorithms, however, are based on kernels. This paper presents persistence indicator functions (PIFs), which summarize persistence diagrams, i.e., feature descriptors in topological data analysis. PIFs can be calculated and compared in linear time and have many beneficial properties, such as the availability of a kernel-based similarity measure. We demonstrate their usage in common data analysis scenarios, such as confidence set estimation and classification of complex structured data.
Persistent Intersection Homology for the Analysis of Discrete Data
Jul 31, 2019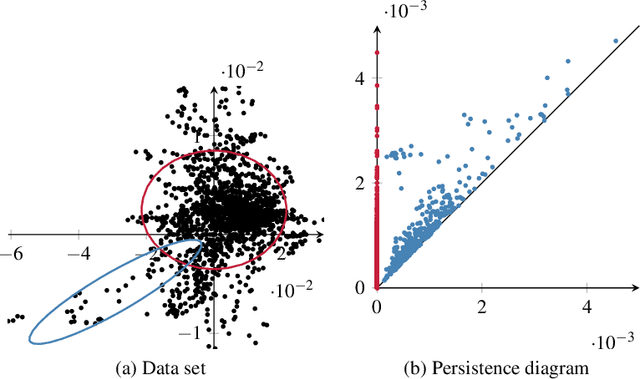

Abstract:Topological data analysis is becoming increasingly relevant to support the analysis of unstructured data sets. A common assumption in data analysis is that the data set is a sample---not necessarily a uniform one---of some high-dimensional manifold. In such cases, persistent homology can be successfully employed to extract features, remove noise, and compare data sets. The underlying problems in some application domains, however, turn out to represent multiple manifolds with different dimensions. Algebraic topology typically analyzes such problems using intersection homology, an extension of homology that is capable of handling configurations with singularities. In this paper, we describe how the persistent variant of intersection homology can be used to assist data analysis in visualization. We point out potential pitfalls in approximating data sets with singularities and give strategies for resolving them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge