Nonlinear Adaptive Algorithms on Rank-One Tensor Models

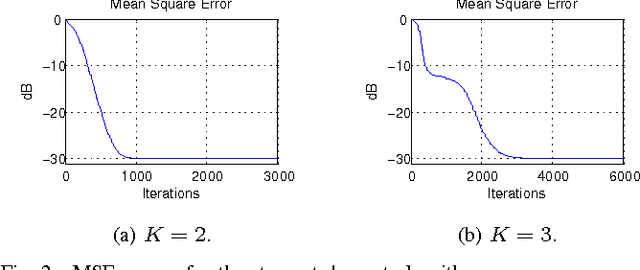
This work proposes a low complexity nonlinearity model and develops adaptive algorithms over it. The model is based on the decomposable---or rank-one, in tensor language---Volterra kernels. It may also be described as a product of FIR filters, which explains its low-complexity. The rank-one model is also interesting because it comes from a well-posed problem in approximation theory. The paper uses such model in an estimation theory context to develop an exact gradient-type algorithm, from which adaptive algorithms such as the least mean squares (LMS) filter and its data-reuse version---the TRUE-LMS---are derived. Stability and convergence issues are addressed. The algorithms are then tested in simulations, which show its good performance when compared to other nonlinear processing algorithms in the literature.

A Nonlinear Adaptive Filter Based on the Model of Simple Multilinear Functionals

Nonlinear adaptive filtering allows for modeling of some additional aspects of a general system and usually relies on highly complex algorithms, such as those based on the Volterra series. Through the use of the Kronecker product and some basic facts of tensor algebra, we propose a simple model of nonlinearity, one that can be interpreted as a product of the outputs of K FIR linear filters, and compute its cost function together with its gradient, which allows for some analysis of the optimization problem. We use these results it in a stochastic gradient framework, from which we derive an LMS-like algorithm and investigate the problems of multi-modality in the mean-square error surface and the choice of adequate initial conditions. Its computational complexity is calculated. The new algorithm is tested in a system identification setup and is compared with other polynomial algorithms from the literature, presenting favorable convergence and/or computational complexity.