Online Learning of Network Bottlenecks via Minimax Paths

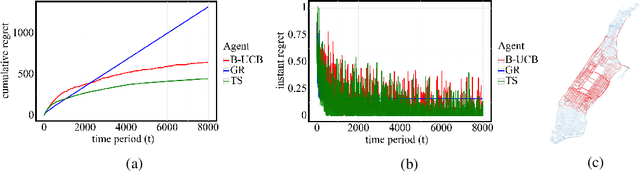
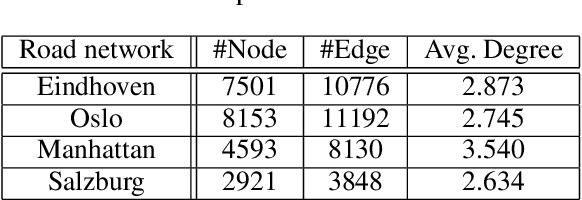
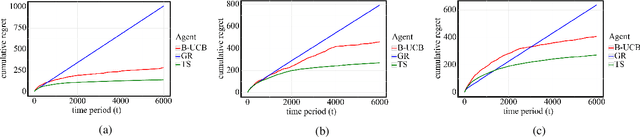
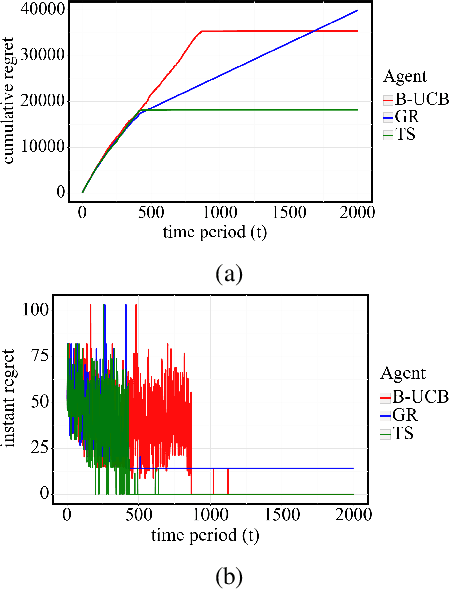
In this paper, we study bottleneck identification in networks via extracting minimax paths. Many real-world networks have stochastic weights for which full knowledge is not available in advance. Therefore, we model this task as a combinatorial semi-bandit problem to which we apply a combinatorial version of Thompson Sampling and establish an upper bound on the corresponding Bayesian regret. Due to the computational intractability of the problem, we then devise an alternative problem formulation which approximates the original objective. Finally, we experimentally evaluate the performance of Thompson Sampling with the approximate formulation on real-world directed and undirected networks.

Memory-Efficient Sampling for Minimax Distance Measures

Minimax distance measure extracts the underlying patterns and manifolds in an unsupervised manner. The existing methods require a quadratic memory with respect to the number of objects. In this paper, we investigate efficient sampling schemes in order to reduce the memory requirement and provide a linear space complexity. In particular, we propose a novel sampling technique that adapts well with Minimax distances. We evaluate the methods on real-world datasets from different domains and analyze the results.