Scaling Intelligence: Designing Data Centers for Next-Gen Language Models

The explosive growth of Large Language Models (LLMs) - such as GPT-4 with 1.8 trillion parameters - demands a radical rethinking of data center architecture to ensure scalability, efficiency, and cost-effectiveness. Our work provides a comprehensive co-design framework that jointly explores FLOPS, HBM bandwidth and capacity, multiple network topologies (two-tier vs. FullFlat optical), the size of the scale-out domain, and popular parallelism/optimization strategies used in LLMs. We introduce and evaluate FullFlat network architectures, which provide uniform high-bandwidth, low-latency connectivity between all nodes, and demonstrate their transformative impact on performance and scalability. Through detailed sensitivity analyses, we quantify the benefits of overlapping compute and communication, leveraging hardware-accelerated collectives, wider scale-out domains, and larger memory capacity. Our study spans both sparse (mixture of experts) and dense transformer-based LLMs, revealing how system design choices affect Model FLOPS Utilization (MFU = Model flops per token x Observed tokens per sec / Peak flops of the hardware) and overall throughput. For the co-design study, we extended and validated a performance modeling tool capable of predicting LLM runtime within 10% of real-world measurements. Our findings offer actionable insights and a practical roadmap for designing AI data centers that can efficiently support trillion-parameter models, reduce optimization complexity, and sustain the rapid evolution of AI capabilities.

Efficient Parallel Multi-Hop Reasoning: A Scalable Approach for Knowledge Graph Analysis

Multi-hop reasoning (MHR) is a process in artificial intelligence and natural language processing where a system needs to make multiple inferential steps to arrive at a conclusion or answer. In the context of knowledge graphs or databases, it involves traversing multiple linked entities and relationships to understand complex queries or perform tasks requiring a deeper understanding. Multi-hop reasoning is a critical function in various applications, including question answering, knowledge base completion, and link prediction. It has garnered significant interest in artificial intelligence, machine learning, and graph analytics. This paper focuses on optimizing MHR for time efficiency on large-scale graphs, diverging from the traditional emphasis on accuracy which is an orthogonal goal. We introduce a novel parallel algorithm that harnesses domain-specific learned embeddings to efficiently identify the top K paths between vertices in a knowledge graph to find the best answers to a three-hop query. Our contributions are: (1) We present a new parallel algorithm to enhance MHR performance, scalability and efficiency. (2) We demonstrate the algorithm's superior performance on leading-edge Intel and AMD architectures through empirical results. We showcase the algorithm's practicality through a case study on identifying academic affiliations of potential Turing Award laureates in Deep Learning, highlighting its capability to handle intricate entity relationships. This demonstrates the potential of our approach to enabling high-performance MHR, useful to navigate the growing complexity of modern knowledge graphs.

A New Parallel Algorithm for Sinkhorn Word-Movers Distance and Its Performance on PIUMA and Xeon CPU

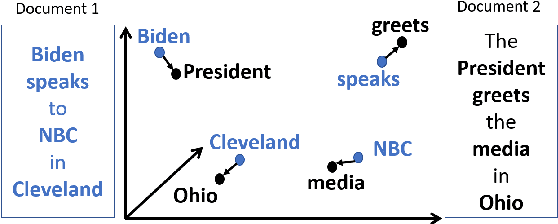
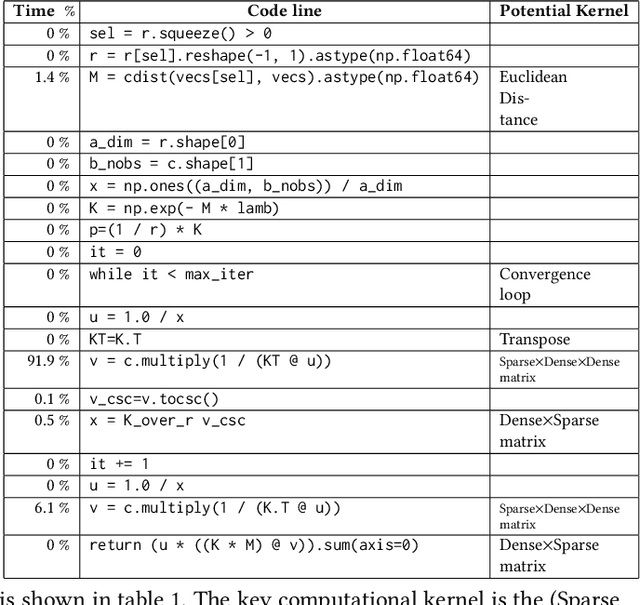
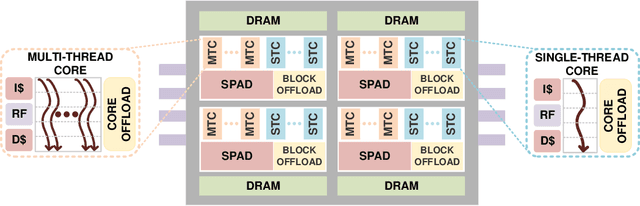
The Word Movers Distance (WMD) measures the semantic dissimilarity between two text documents by computing the cost of optimally moving all words of a source/query document to the most similar words of a target document. Computing WMD between two documents is costly because it requires solving an optimization problem that costs $O (V^3 \log(V)) $ where $V$ is the number of unique words in the document. Fortunately, WMD can be framed as an Earth Mover's Distance (EMD) for which the algorithmic complexity can be reduced to $O(V^2)$ by adding an entropy penalty to the optimization problem and solving it using the Sinkhorn-Knopp algorithm. Additionally, the computation can be made highly parallel by computing the WMD of a single query document against multiple target documents at once, for example by finding whether a given tweet is similar to any other tweets of a given day. In this paper, we first present a shared-memory parallel Sinkhorn-Knopp algorithm to compute the WMD of one document against many other documents by adopting the $ O(V^2)$ EMD algorithm. We then algorithmically transform the original $O(V^2)$ dense compute-heavy version into an equivalent sparse one which is mapped onto the new Intel Programmable Integrated Unified Memory Architecture (PIUMA) system. The WMD parallel implementation achieves 67x speedup on 96 cores across 4 NUMA sockets of an Intel Cascade Lake system. We also show that PIUMA cores are around 1.2-2.6x faster than Xeon cores on Sinkhorn-WMD and also provide better strong scaling.

An Efficient Shared-memory Parallel Sinkhorn-Knopp Algorithm to Compute the Word Mover's Distance

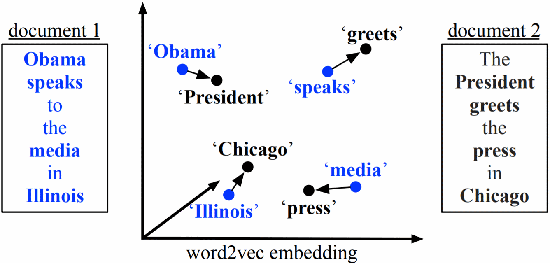
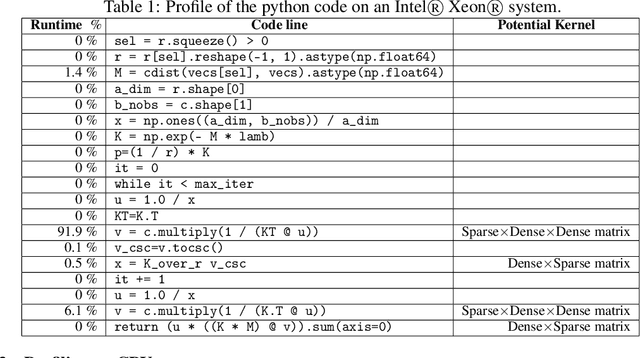
The Word Mover's Distance (WMD) is a metric that measures the semantic dissimilarity between two text documents by computing the cost of moving all words of a source/query document to the most similar words of a target document optimally. Computing WMD between two documents is costly because it requires solving an optimization problem that costs \(O(V^3log(V))\) where \(V\) is the number of unique words in the document. Fortunately, the WMD can be framed as the Earth Mover's Distance (EMD) (also known as the Optimal Transportation Distance) for which it has been shown that the algorithmic complexity can be reduced to \(O(V^2)\) by adding an entropy penalty to the optimization problem and a similar idea can be adapted to compute WMD efficiently. Additionally, the computation can be made highly parallel by computing WMD of a single query document against multiple target documents at once (e.g., finding whether a given tweet is similar to any other tweets happened in a day). In this paper, we present a shared-memory parallel Sinkhorn-Knopp Algorithm to compute the WMD of one document against many other documents by adopting the \(O(V^2)\) EMD algorithm. We used algorithmic transformations to change the original dense compute-heavy kernel to a sparse compute kernel and obtained \(67\times\) speedup using \(96\) cores on the state-of-the-art of Intel\textregistered{} 4-sockets Cascade Lake machine w.r.t. its sequential run. Our parallel algorithm is over \(700\times\) faster than the naive parallel python code that internally uses optimized matrix library calls.

Online and Real-time Object Tracking Algorithm with Extremely Small Matrices

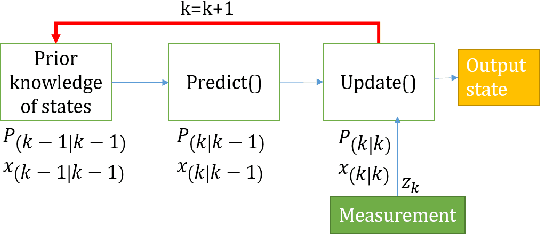
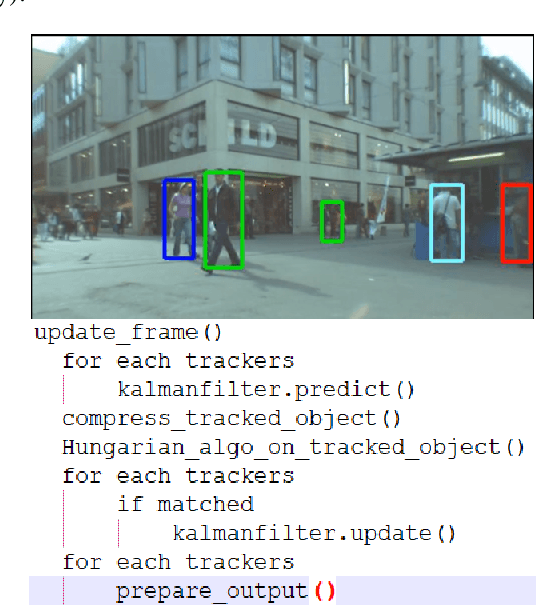
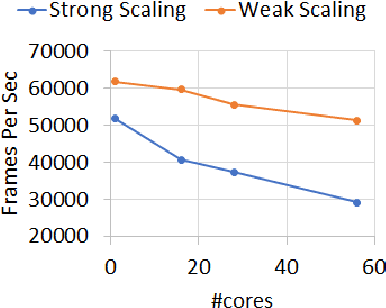
Online and Real-time Object Tracking is an interesting workload that can be used to track objects (e.g., car, human, animal) in a series of video sequences in real-time. For simple object tracking on edge devices, the output of object tracking could be as simple as drawing a bounding box around a detected object and in some cases, the input matrices used in such computation are quite small (e.g., 4x7, 3x3, 5x5, etc). As a result, the amount of actual work is low. Therefore, a typical multi-threading based parallelization technique can not accelerate the tracking application; instead, a throughput based parallelization technique where each thread operates on independent video sequences is more rewarding. In this paper, we share our experience in parallelizing a Simple Online and Real-time Tracking (SORT) application on shared-memory multicores.