A New Parallel Algorithm for Sinkhorn Word-Movers Distance and Its Performance on PIUMA and Xeon CPU

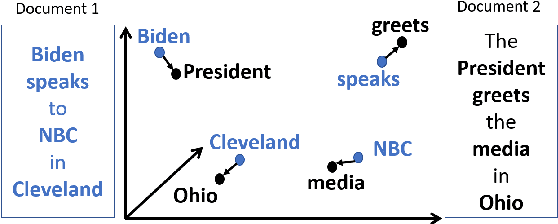
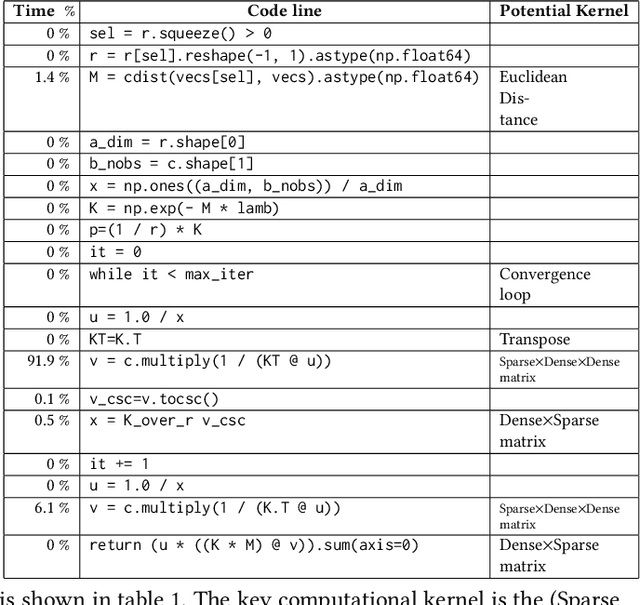
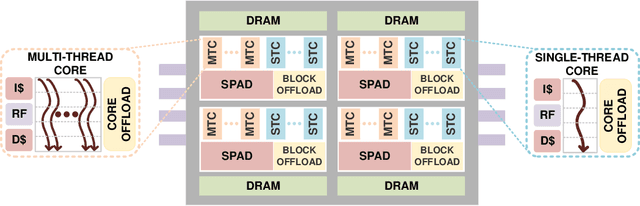
The Word Movers Distance (WMD) measures the semantic dissimilarity between two text documents by computing the cost of optimally moving all words of a source/query document to the most similar words of a target document. Computing WMD between two documents is costly because it requires solving an optimization problem that costs $O (V^3 \log(V)) $ where $V$ is the number of unique words in the document. Fortunately, WMD can be framed as an Earth Mover's Distance (EMD) for which the algorithmic complexity can be reduced to $O(V^2)$ by adding an entropy penalty to the optimization problem and solving it using the Sinkhorn-Knopp algorithm. Additionally, the computation can be made highly parallel by computing the WMD of a single query document against multiple target documents at once, for example by finding whether a given tweet is similar to any other tweets of a given day. In this paper, we first present a shared-memory parallel Sinkhorn-Knopp algorithm to compute the WMD of one document against many other documents by adopting the $ O(V^2)$ EMD algorithm. We then algorithmically transform the original $O(V^2)$ dense compute-heavy version into an equivalent sparse one which is mapped onto the new Intel Programmable Integrated Unified Memory Architecture (PIUMA) system. The WMD parallel implementation achieves 67x speedup on 96 cores across 4 NUMA sockets of an Intel Cascade Lake system. We also show that PIUMA cores are around 1.2-2.6x faster than Xeon cores on Sinkhorn-WMD and also provide better strong scaling.