Exponential tilting of subweibull distributions

The class of subweibull distributions has recently been shown to generalize the important properties of subexponential and subgaussian random variables. We describe alternative characterizations of subweibull distributions and detail the conditions under which their tail behavior is preserved after exponential tilting.

Correcting for heterogeneity in real-time epidemiological indicators

Auxiliary data sources have become increasingly important in epidemiological surveillance, as they are often available at a finer spatial and temporal resolution, larger coverage, and lower latency than traditional surveillance signals. We describe the problem of spatial and temporal heterogeneity in these signals derived from these data sources, where spatial and/or temporal biases are present. We present a method to use a ``guiding'' signal to correct for these biases and produce a more reliable signal that can be used for modeling and forecasting. The method assumes that the heterogeneity can be approximated by a low-rank matrix and that the temporal heterogeneity is smooth over time. We also present a hyperparameter selection algorithm to choose the parameters representing the matrix rank and degree of temporal smoothness of the corrections. In the absence of ground truth, we use maps and plots to argue that this method does indeed reduce heterogeneity. Reducing heterogeneity from auxiliary data sources greatly increases their utility in modeling and forecasting epidemics.

Nonnegative spatial factorization

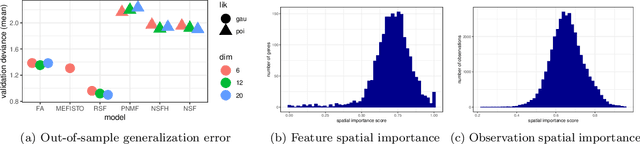
Gaussian processes are widely used for the analysis of spatial data due to their nonparametric flexibility and ability to quantify uncertainty, and recently developed scalable approximations have facilitated application to massive datasets. For multivariate outcomes, linear models of coregionalization combine dimension reduction with spatial correlation. However, their real-valued latent factors and loadings are difficult to interpret because, unlike nonnegative models, they do not recover a parts-based representation. We present nonnegative spatial factorization (NSF), a spatially-aware probabilistic dimension reduction model that naturally encourages sparsity. We compare NSF to real-valued spatial factorizations such as MEFISTO and nonspatial dimension reduction methods using simulations and high-dimensional spatial transcriptomics data. NSF identifies generalizable spatial patterns of gene expression. Since not all patterns of gene expression are spatial, we also propose a hybrid extension of NSF that combines spatial and nonspatial components, enabling quantification of spatial importance for both observations and features. A TensorFlow implementation of NSF is available from https://github.com/willtownes/nsf-paper .

Review of Probability Distributions for Modeling Count Data

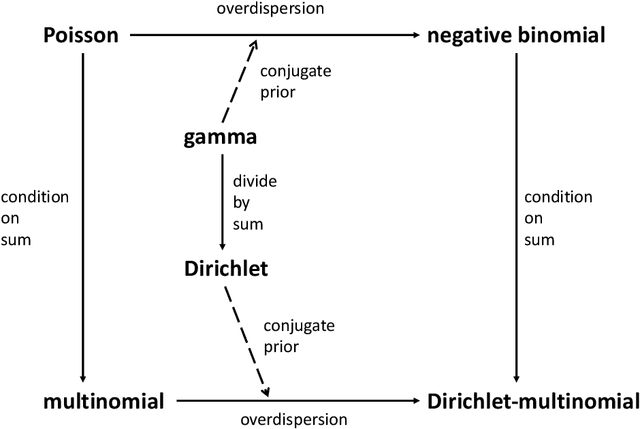
Count data take on non-negative integer values and are challenging to properly analyze using standard linear-Gaussian methods such as linear regression and principal components analysis. Generalized linear models enable direct modeling of counts in a regression context using distributions such as the Poisson and negative binomial. When counts contain only relative information, multinomial or Dirichlet-multinomial models can be more appropriate. We review some of the fundamental connections between multinomial and count models from probability theory, providing detailed proofs. These relationships are useful for methods development in applications such as topic modeling of text data and genomics.

Generalized Principal Component Analysis

Generalized principal component analysis (GLM-PCA) facilitates dimension reduction of non-normally distributed data. We provide a detailed derivation of GLM-PCA with a focus on optimization. We also demonstrate how to incorporate covariates, and suggest post-processing transformations to improve interpretability of latent factors.