Discovering the Graph Structure in the Clustering Results

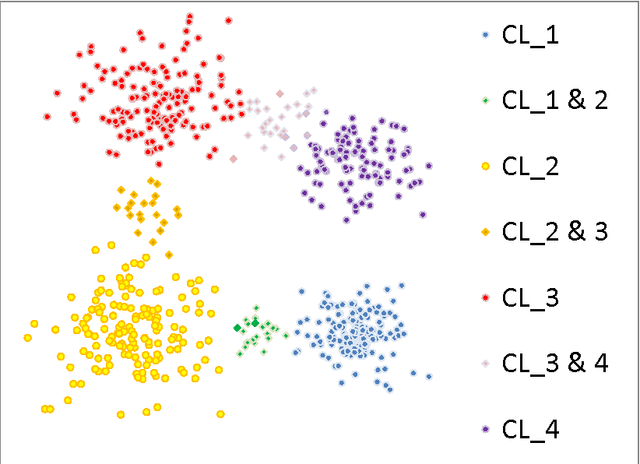
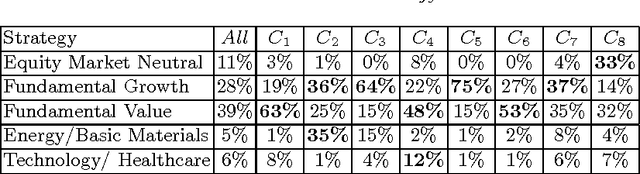
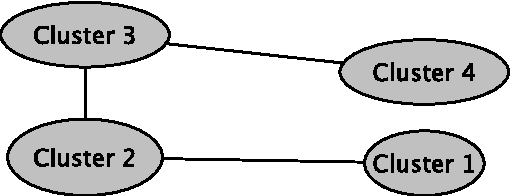
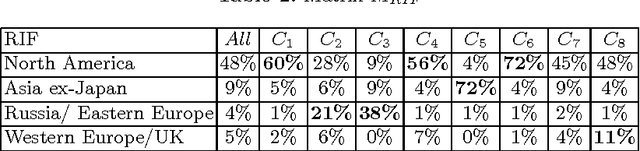
In a standard cluster analysis, such as k-means, in addition to clusters locations and distances between them, it's important to know if they are connected or well separated from each other. The main focus of this paper is discovering the relations between the resulting clusters. We propose a new method which is based on pairwise overlapping k-means clustering, that in addition to means of clusters provides the graph structure of their relations. The proposed method has a set of parameters that can be tuned in order to control the sensitivity of the model and the desired relative size of the pairwise overlapping interval between means of two adjacent clusters, i.e., level of overlapping. We present the exact formula for calculating that parameter. The empirical study presented in the paper demonstrates that our approach works well not only on toy data but also compliments standard clustering results with a reasonable graph structure on real datasets, such as financial indices and restaurants.

One-Class Semi-Supervised Learning: Detecting Linearly Separable Class by its Mean

In this paper, we presented a novel semi-supervised one-class classification algorithm which assumes that class is linearly separable from other elements. We proved theoretically that class is linearly separable if and only if it is maximal by probability within the sets with the same mean. Furthermore, we presented an algorithm for identifying such linearly separable class utilizing linear programming. We described three application cases including an assumption of linear separability, Gaussian distribution, and the case of linear separability in transformed space of kernel functions. Finally, we demonstrated the work of the proposed algorithm on the USPS dataset and analyzed the relationship of the performance of the algorithm and the size of the initially labeled sample.