Jacobian Regularization Stabilizes Long-Term Integration of Neural Differential Equations

Hybrid models and Neural Differential Equations (NDE) are getting increasingly important for the modeling of physical systems, however they often encounter stability and accuracy issues during long-term integration. Training on unrolled trajectories is known to limit these divergences but quickly becomes too expensive due to the need for computing gradients over an iterative process. In this paper, we demonstrate that regularizing the Jacobian of the NDE model via its directional derivatives during training stabilizes long-term integration in the challenging context of short training rollouts. We design two regularizations, one for the case of known dynamics where we can directly derive the directional derivatives of the dynamic and one for the case of unknown dynamics where they are approximated using finite differences. Both methods, while having a far lower cost compared to long rollouts during training, are successful in improving the stability of long-term simulations for several ordinary and partial differential equations, opening up the door to training NDE methods for long-term integration of large scale systems.

Koopman Autoencoders with Continuous-Time Latent Dynamics for Fluid Dynamics Forecasting

Data-driven surrogate models have emerged as powerful tools for accelerating the simulation of turbulent flows. However, classical approaches which perform autoregressive rollouts often trade off between strong short-term accuracy and long-horizon stability. Koopman autoencoders, inspired by Koopman operator theory, provide a physics-based alternative by mapping nonlinear dynamics into a latent space where linear evolution is conducted. In practice, most existing formulations operate in a discrete-time setting, limiting temporal flexibility. In this work, we introduce a continuous-time Koopman framework that models latent evolution through numerical integration schemes. By allowing variable timesteps at inference, the method demonstrates robustness to temporal resolution and generalizes beyond training regimes. In addition, the learned dynamics closely adhere to the analytical matrix exponential solution, enabling efficient long-horizon forecasting. We evaluate the approach on classical CFD benchmarks and report accuracy, stability, and extrapolation properties.

Learning to generate physical ocean states: Towards hybrid climate modeling

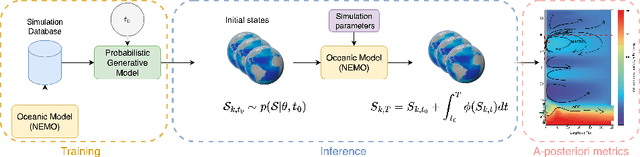
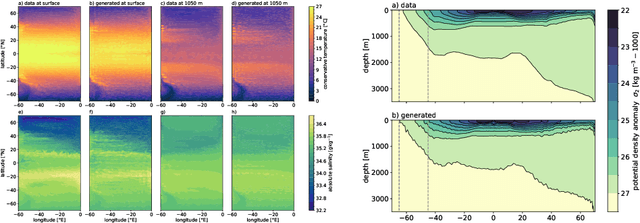
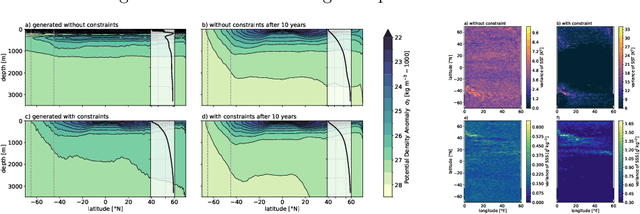
Ocean General Circulation Models require extensive computational resources to reach equilibrium states, while deep learning emulators, despite offering fast predictions, lack the physical interpretability and long-term stability necessary for climate scientists to understand climate sensitivity (to greenhouse gas emissions) and mechanisms of abrupt % variability such as tipping points. We propose to take the best from both worlds by leveraging deep generative models to produce physically consistent oceanic states that can serve as initial conditions for climate projections. We assess the viability of this hybrid approach through both physical metrics and numerical experiments, and highlight the benefits of enforcing physical constraints during generation. Although we train here on ocean variables from idealized numerical simulations, we claim that this hybrid approach, combining the computational efficiency of deep learning with the physical accuracy of numerical models, can effectively reduce the computational burden of running climate models to equilibrium, and reduce uncertainties in climate projections by minimizing drifts in baseline simulations.

Unsupervised motion segmentation in one go: Smooth long-term model over a video

Human beings have the ability to continuously analyze a video and immediately extract the main motion components. Motion segmentation methods often proceed frame by frame. We want to go beyond this classical paradigm, and perform the motion segmentation over a video sequence in one go. It will be a prominent added value for downstream computer vision tasks, and could provide a pretext criterion for unsupervised video representation learning. In this perspective, we propose a novel long-term spatio-temporal model operating in a totally unsupervised way. It takes as input the volume of consecutive optical flow (OF) fields, and delivers a volume of segments of coherent motion over the video. More specifically, we have designed a transformer-based network, where we leverage a mathematically well-founded framework, the Evidence Lower Bound (ELBO), to infer the loss function. The loss function combines a flow reconstruction term involving spatio-temporal parametric motion models combining, in a novel way, polynomial (quadratic) motion models for the $(x,y)$-spatial dimensions and B-splines for the time dimension of the video sequence, and a regularization term enforcing temporal consistency on the masks. We report experiments on four VOS benchmarks with convincing quantitative results. We also highlight through visual results the key contributions on temporal consistency brought by our method.

EM-driven unsupervised learning for efficient motion segmentation

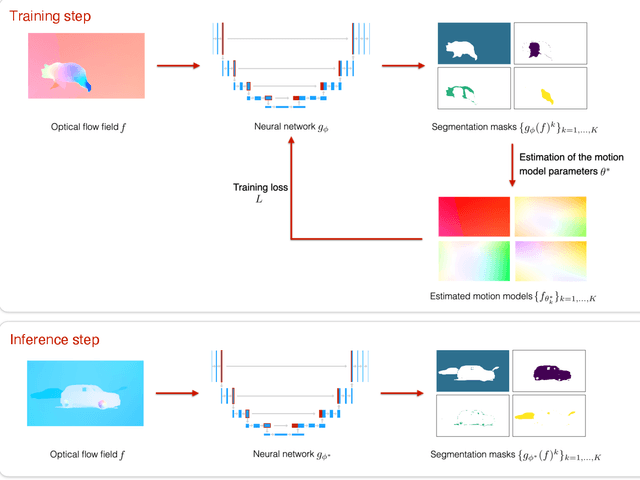
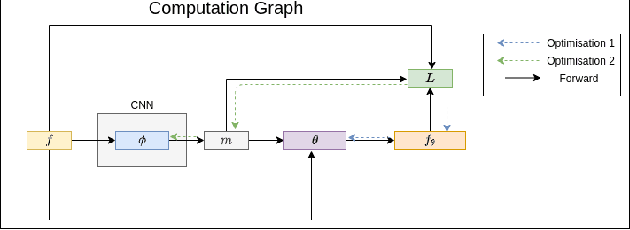
This paper presents a CNN-based fully unsupervised method for motion segmentation from optical flow. We assume that the input optical flow can be represented as a piecewise set of parametric motion models, typically, affine or quadratic motion models.The core idea of this work is to leverage the Expectation-Maximization (EM) framework. It enables us to design in a well-founded manner the loss function and the training procedure of our motion segmentation neural network. However, in contrast to the classical iterative EM, once the network is trained, we can provide a segmentation for any unseen optical flow field in a single inference step, with no dependence on the initialization of the motion model parameters since they are not estimated in the inference stage. Different loss functions have been investigated including robust ones. We also propose a novel data augmentation technique on the optical flow field with a noticeable impact on the performance. We tested our motion segmentation network on the DAVIS2016 dataset. Our method outperforms comparable unsupervised methods and is very efficient. Indeed, it can run at 125fps making it usable for real-time applications.