Weakly synchronous systems with three machines are Turing powerful

Communicating finite-state machines (CFMs) are a Turing powerful model of asynchronous message-passing distributed systems. In weakly synchronous systems, processes communicate through phases in which messages are first sent and then received, for each process. Such systems enjoy a limited form of synchronization, and for some communication models, this restriction is enough to make the reachability problem decidable. In particular, we explore the intriguing case of p2p (FIFO) communication, for which the reachability problem is known to be undecidable for four processes, but decidable for two. We show that the configuration reachability problem for weakly synchronous systems of three processes is undecidable. This result is heavily inspired by our study on the treewidth of the Message Sequence Charts (MSCs) that might be generated by such systems. In this sense, the main contribution of this work is a weakly synchronous system with three processes that generates MSCs of arbitrarily large treewidth.

A non-sequential hierarchy of message-passing models

There is a wide variety of message-passing communication models, ranging from synchronous ''rendez-vous'' communications to fully asynchronous/out-of-order communications. For large-scale distributed systems, the communication model is determined by the transport layer of the network, and a few classes of orders of message delivery (FIFO, causally ordered) have been identified in the early days of distributed computing. For local-scale message-passing applications, e.g., running on a single machine, the communication model may be determined by the actual implementation of message buffers and by how FIFO queues are used. While large-scale communication models, such as causal ordering, are defined by logical axioms, local-scale models are often defined by an operational semantics. In this work, we connect these two approaches, and we present a unified hierarchy of communication models encompassing both large-scale and local-scale models, based on their non-sequential behaviors. We also show that all the communication models we consider can be axiomatised in the monadic second order logic, and may therefore benefit from several bounded verification techniques based on bounded special treewidth. CCS Concepts: $\bullet$ Theory of computation $\rightarrow$ Verification by model checking; Modal and temporal logics; Distributed computing models.

On the k-synchronizability for mailbox systems

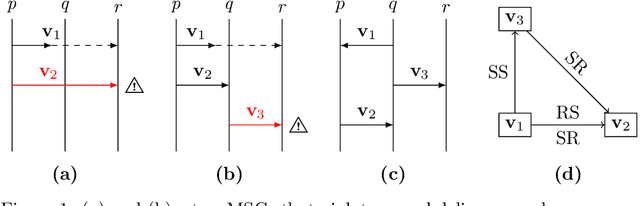
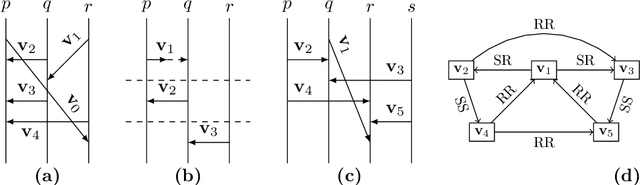
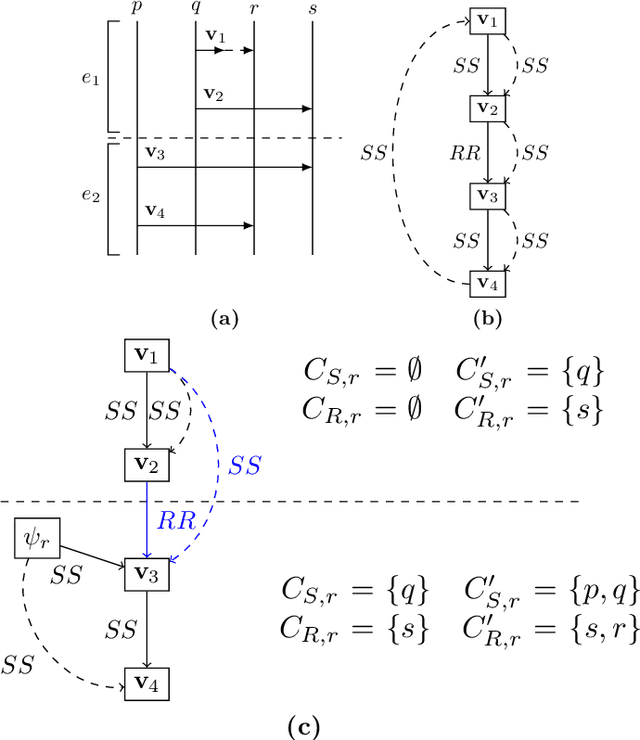
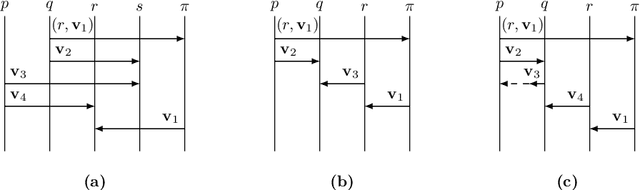
Asynchronous bounded or unbounded message passing is ubiquitous in communication-centric systems. When modelling distributed scenarios, it is important to understand whether buffers are bounded or not. In this paper, we work on the notion of k-synchronizability: a system is k-synchronizable if any of its executions, up to reordering causally independent actions, can be divided into a succession of k-bounded interaction phases. We show two results: first, the reachability problem is decidable for k-synchronizable systems; second, the membership problem (whether a given system is k-synchronizable) is decidable as well. Our proofs fix several important issues in previous attempts to prove these two results.