A representational framework for learning and encoding structurally enriched trajectories in complex agent environments

The ability of artificial intelligence agents to make optimal decisions and generalise them to different domains and tasks is compromised in complex scenarios. One way to address this issue has focused on learning efficient representations of the world and on how the actions of agents affect them, such as disentangled representations that exploit symmetries. Whereas such representations are procedurally efficient, they are based on the compression of low-level state-action transitions, which lack structural richness. To address this problem, we propose to enrich the agent's ontology and extend the traditional conceptualisation of trajectories to provide a more nuanced view of task execution. Structurally Enriched Trajectories (SETs) extend the encoding of sequences of states and their transitions by incorporating hierarchical relations between objects, interactions and affordances. SETs are built as multi-level graphs, providing a detailed representation of the agent dynamics and a transferable functional abstraction of the task. SETs are integrated into an architecture, Structurally Enriched Trajectory Learning and Encoding (SETLE), that employs a heterogeneous graph-based memory structure of multi-level relational dependencies essential for generalisation. Using reinforcement learning as a data generation tool, we demonstrate that SETLE can support downstream tasks, enabling agents to recognise task-relevant structural patterns across diverse environments.

Algebras of actions in an agent's representations of the world

In this paper, we propose a framework to extract the algebra of the transformations of worlds from the perspective of an agent. As a starting point, we use our framework to reproduce the symmetry-based representations from the symmetry-based disentangled representation learning (SBDRL) formalism proposed by [1]; only the algebra of transformations of worlds that form groups can be described using symmetry-based representations. We then study the algebras of the transformations of worlds with features that occur in simple reinforcement learning scenarios. Using computational methods, that we developed, we extract the algebras of the transformations of these worlds and classify them according to their properties. Finally, we generalise two important results of SBDRL - the equivariance condition and the disentangling definition - from only working with symmetry-based representations to working with representations capturing the transformation properties of worlds with transformations for any algebra. Finally, we combine our generalised equivariance condition and our generalised disentangling definition to show that disentangled sub-algebras can each have their own individual equivariance conditions, which can be treated independently.

AIGenC: AI generalisation via creativity

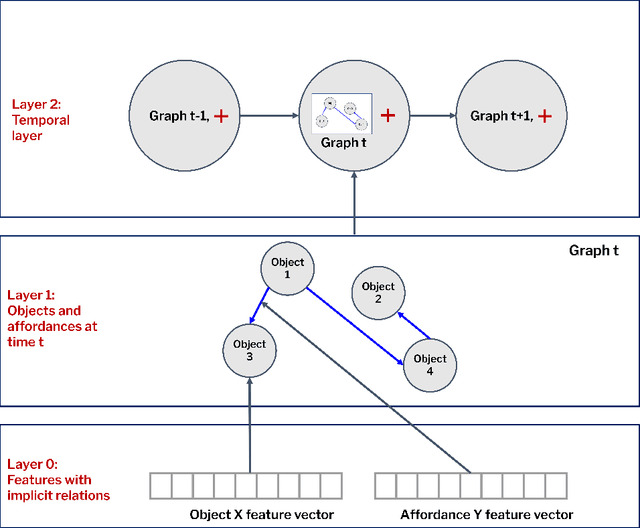
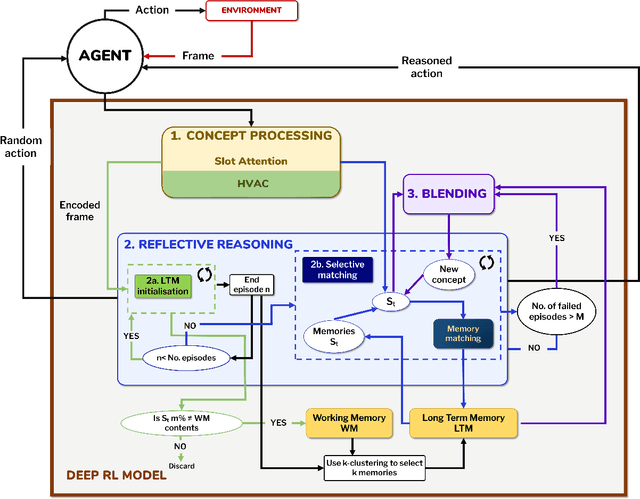
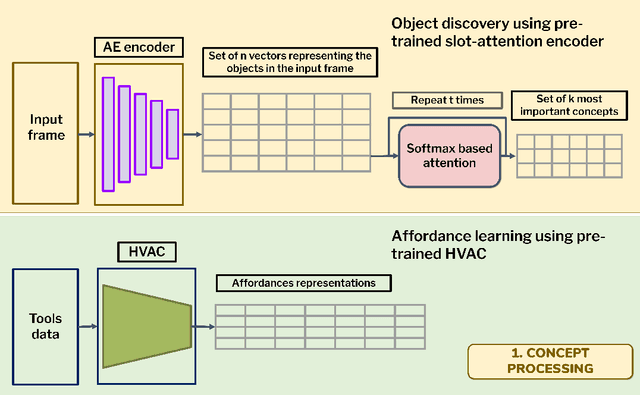
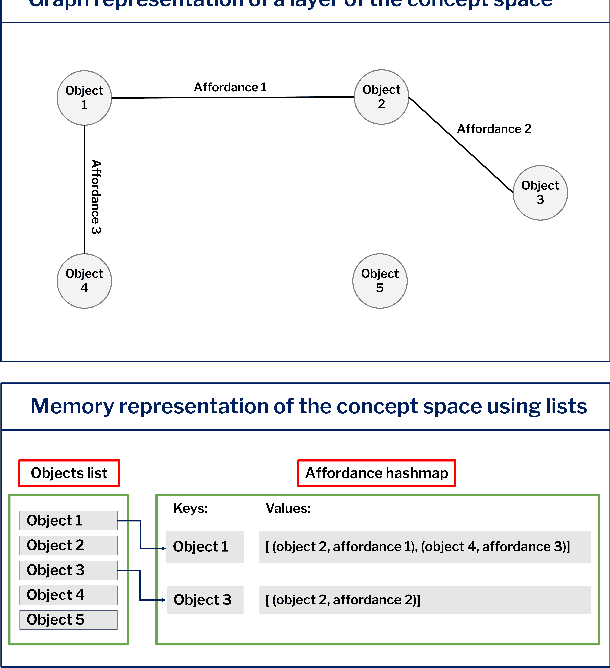
This paper introduces a computational model of creative problem solving in deep reinforcement learning agents, inspired by cognitive theories of creativity. The AIGenC model aims at enabling artificial agents to learn, use and generate transferable representations. AIGenC is embedded in a deep learning architecture that includes three main components: concept processing, reflective reasoning, and blending of concepts. The first component extracts objects and affordances from sensory input and encodes them in a concept space, represented as a hierarchical graph structure. Concept representations are stored in a dual memory system. Goal-directed and temporal information acquired by the agent during deep reinforcement learning enriches the representations creating a higher-level of abstraction in the concept space. In parallel, a process akin to reflective reasoning detects and recovers from memory concepts relevant to the task according to a matching process that calculates a similarity value between the current state and memory graph structures. Once an interaction is finalised, rewards and temporal information are added to the graph structure, creating a higher abstraction level. If reflective reasoning fails to offer a suitable solution, a blending process comes into place to create new concepts by combining past information. We discuss the model's capability to yield better out-of-distribution generalisation in artificial agents, thus advancing toward artificial general intelligence. To the best of our knowledge, this is the first computational model, beyond mere formal theories, that posits a solution to creative problem solving within a deep learning architecture.