Footstep Adjustment for Biped Push Recovery on Slippery Surfaces

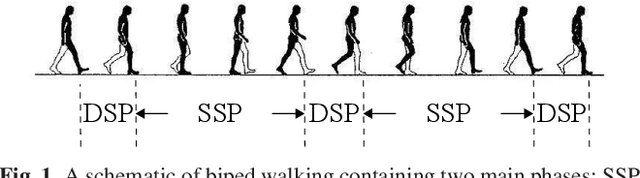
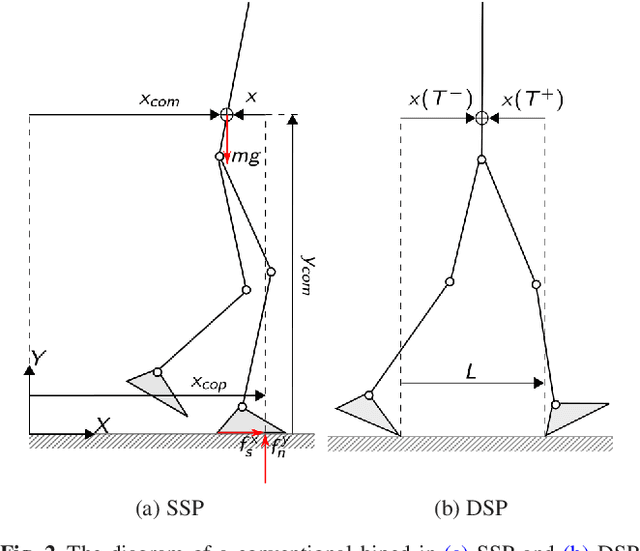
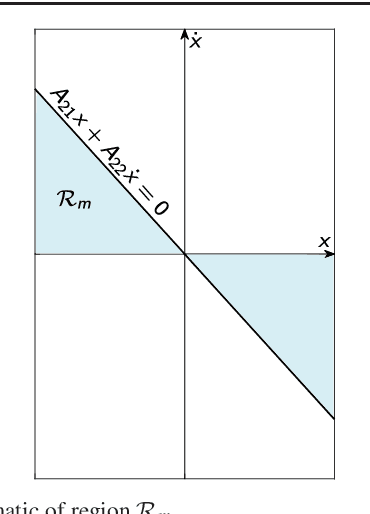
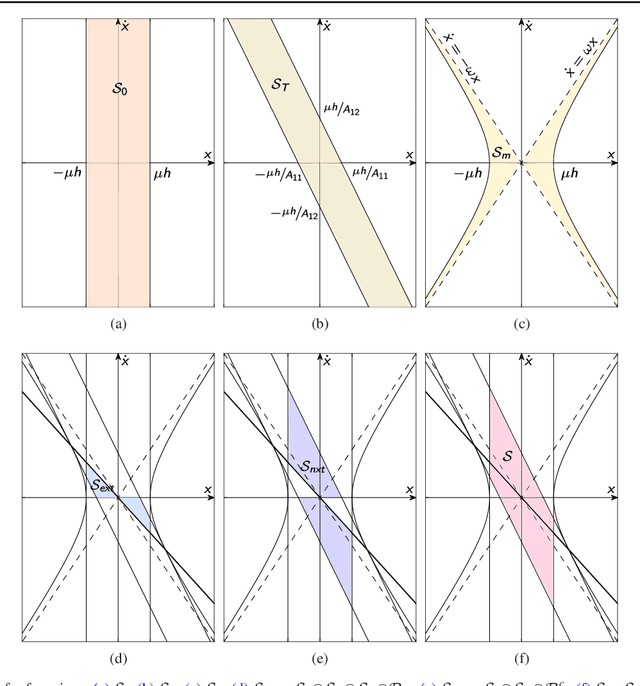
Despite extensive studies on motion stabilization of bipeds, they still suffer from the lack of disturbance coping capability on slippery surfaces. In this paper, a novel controller for stabilizing a bipedal motion in its sagittal plane is developed with regard to the surface friction limitations. By taking into account the physical limitation of the surface in the stabilization trend, a more advanced level of reliability is achieved that provides higher functionalities such as push recovery on low-friction surfaces and prevents the stabilizer from overreacting. The discrete event-based strategy consists of modifying the step length and time period at the beginning of each footstep in order to reestablish stability necessary conditions while taking into account the surface friction limitation as a constraint to prevent slippage. Adjusting footsteps to prevent slippage in confronting external disturbances is perceived as a novel strategy for keeping stability, quite similar to human reaction. The developed methodology consists of rough closed-form solutions utilizing elementary math operations for obtaining the control inputs, allowing to reach a balance between convergence and computational cost, which is quite suitable for real-time operations even with modest computational hardware. Several numerical simulations, including push recovery and switching between different gates on low-friction surfaces, are performed to demonstrate the effectiveness of the proposed controller. In correlation with human-gait experience, the results also reveal some physical aspects favoring stability and the fact of switching between gaits to reduce the risk of falling in confronting different conditions.

Stabilization of Bipedal Robot Motion based on Total Momentum

Bipedal robots adapt to the environment of the modern society due to the similarity of movement to humans, and therefore they are a good partner for humans. However, maintaining the stability of these robots during walking/running motion is a challenging issue that, despite the development of new technologies and the advancement of knowledge, does not yet have a satisfactory solution. In most of the proposed methods by researchers, to maintain the stability of walking bipedal robots, it has been tried to ensure the momentary stability of motion by limiting the motion to multiple constraints. Although these methods have good performance in sustaining stability, they leave the robot away from the natural movement of humans, with low efficiency and high energy consumption. Hence, many researchers have turned to the walking techniques that follow a certain motion limit cycle, in which we can consider the overall stability rather than momentary. In this paper, a method is proposed to maintain the stability of the limit cycle against disturbance. For this purpose, the dynamical model of the biped robot is extracted in the space of total momentum variables and, according to the desired step length and speed, the motion limit cycle is designed. Subsequently, a motion stabilizer is proposed based on the idea of length shift, which is a natural human strategy for sustaining the balance in case of impact. The simulations show that this technique has a good performance in maintaining the stability of motion and has similar responses to human response.