Egor Danilov
Neural Inference of Gaussian Processes for Time Series Data of Quasars
Nov 17, 2022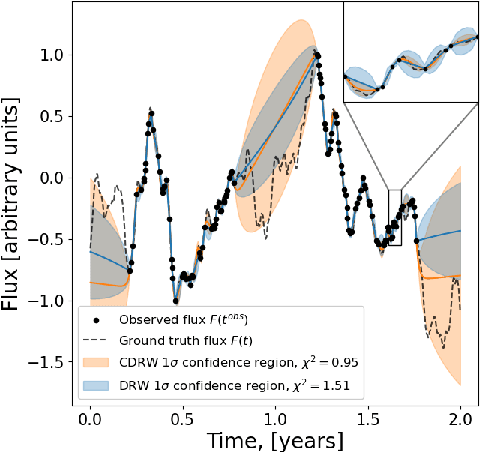

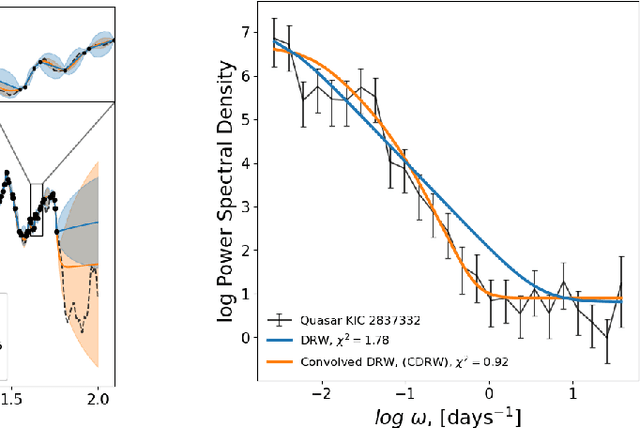

Abstract:The study of quasar light curves poses two problems: inference of the power spectrum and interpolation of an irregularly sampled time series. A baseline approach to these tasks is to interpolate a time series with a Damped Random Walk (DRW) model, in which the spectrum is inferred using Maximum Likelihood Estimation (MLE). However, the DRW model does not describe the smoothness of the time series, and MLE faces many problems in terms of optimization and numerical precision. In this work, we introduce a new stochastic model that we call $\textit{Convolved Damped Random Walk}$ (CDRW). This model introduces a concept of smoothness to a DRW, which enables it to describe quasar spectra completely. We also introduce a new method of inference of Gaussian process parameters, which we call $\textit{Neural Inference}$. This method uses the powers of state-of-the-art neural networks to improve the conventional MLE inference technique. In our experiments, the Neural Inference method results in significant improvement over the baseline MLE (RMSE: $0.318 \rightarrow 0.205$, $0.464 \rightarrow 0.444$). Moreover, the combination of both the CDRW model and Neural Inference significantly outperforms the baseline DRW and MLE in interpolating a typical quasar light curve ($\chi^2$: $0.333 \rightarrow 0.998$, $2.695 \rightarrow 0.981$). The code is published on GitHub.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge