Function-Space Learning Rates

We consider layerwise function-space learning rates, which measure the magnitude of the change in a neural network's output function in response to an update to a parameter tensor. This contrasts with traditional learning rates, which describe the magnitude of changes in parameter space. We develop efficient methods to measure and set function-space learning rates in arbitrary neural networks, requiring only minimal computational overhead through a few additional backward passes that can be performed at the start of, or periodically during, training. We demonstrate two key applications: (1) analysing the dynamics of standard neural network optimisers in function space, rather than parameter space, and (2) introducing FLeRM (Function-space Learning Rate Matching), a novel approach to hyperparameter transfer across model scales. FLeRM records function-space learning rates while training a small, cheap base model, then automatically adjusts parameter-space layerwise learning rates when training larger models to maintain consistent function-space updates. FLeRM gives hyperparameter transfer across model width, depth, initialisation scale, and LoRA rank in various architectures including MLPs with residual connections and transformers with different layer normalisation schemes.

Stochastic Kernel Regularisation Improves Generalisation in Deep Kernel Machines

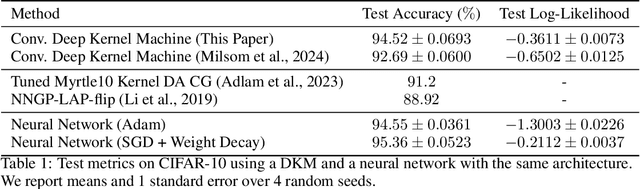
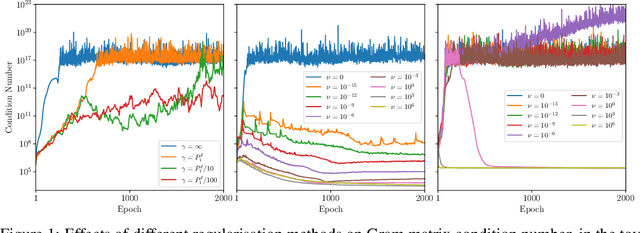
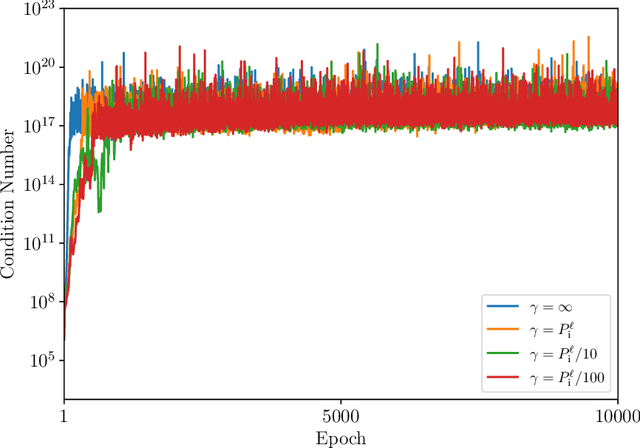
Recent work developed convolutional deep kernel machines, achieving 92.7% test accuracy on CIFAR-10 using a ResNet-inspired architecture, which is SOTA for kernel methods. However, this still lags behind neural networks, which easily achieve over 94% test accuracy with similar architectures. In this work we introduce several modifications to improve the convolutional deep kernel machine's generalisation, including stochastic kernel regularisation, which adds noise to the learned Gram matrices during training. The resulting model achieves 94.5% test accuracy on CIFAR-10. This finding has important theoretical and practical implications, as it demonstrates that the ability to perform well on complex tasks like image classification is not unique to neural networks. Instead, other approaches including deep kernel methods can achieve excellent performance on such tasks, as long as they have the capacity to learn representations from data.

Flexible infinite-width graph convolutional networks and the importance of representation learning

A common theoretical approach to understanding neural networks is to take an infinite-width limit, at which point the outputs become Gaussian process (GP) distributed. This is known as a neural network Gaussian process (NNGP). However, the NNGP kernel is fixed, and tunable only through a small number of hyperparameters, eliminating any possibility of representation learning. This contrasts with finite-width NNs, which are often believed to perform well precisely because they are able to learn representations. Thus in simplifying NNs to make them theoretically tractable, NNGPs may eliminate precisely what makes them work well (representation learning). This motivated us to understand whether representation learning is necessary in a range of graph classification tasks. We develop a precise tool for this task, the graph convolutional deep kernel machine. This is very similar to an NNGP, in that it is an infinite width limit and uses kernels, but comes with a `knob' to control the amount of representation learning. We found that representation learning is necessary (in the sense that it gives dramatic performance improvements) in graph classification tasks and heterophilous node classification tasks, but not in homophilous node classification tasks.

Convolutional Deep Kernel Machines

Deep kernel machines (DKMs) are a recently introduced kernel method with the flexibility of other deep models including deep NNs and deep Gaussian processes. DKMs work purely with kernels, never with features, and are therefore different from other methods ranging from NNs to deep kernel learning and even deep Gaussian processes, which all use features as a fundamental component. Here, we introduce convolutional DKMs, along with an efficient inter-domain inducing point approximation scheme. Further, we develop and experimentally assess a number of model variants, including 9 different types of normalisation designed for the convolutional DKMs, two likelihoods, and two different types of top-layer. The resulting models achieve around 99% test accuracy on MNIST, 92% on CIFAR-10 and 71% on CIFAR-100, despite training in only around 28 GPU hours, 1-2 orders of magnitude faster than full NNGP / NTK / Myrtle kernels, whilst achieving comparable performance.

An Improved Variational Approximate Posterior for the Deep Wishart Process

Deep kernel processes are a recently introduced class of deep Bayesian models that have the flexibility of neural networks, but work entirely with Gram matrices. They operate by alternately sampling a Gram matrix from a distribution over positive semi-definite matrices, and applying a deterministic transformation. When the distribution is chosen to be Wishart, the model is called a deep Wishart process (DWP). This particular model is of interest because its prior is equivalent to a deep Gaussian process (DGP) prior, but at the same time it is invariant to rotational symmetries, leading to a simpler posterior distribution. Practical inference in the DWP was made possible in recent work ("A variational approximate posterior for the deep Wishart process" Ober and Aitchison 2021a) where the authors used a generalisation of the Bartlett decomposition of the Wishart distribution as the variational approximate posterior. However, predictive performance in that paper was less impressive than one might expect, with the DWP only beating a DGP on a few of the UCI datasets used for comparison. In this paper, we show that further generalising their distribution to allow linear combinations of rows and columns in the Bartlett decomposition results in better predictive performance, while incurring negligible additional computation cost.