Nonsmooth Frank-Wolfe using Uniform Affine Approximations

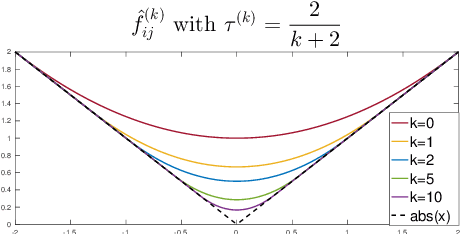
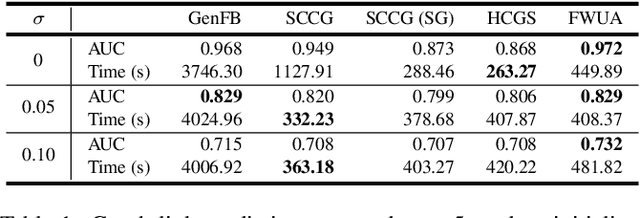
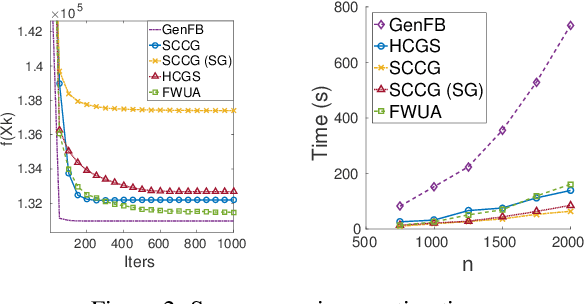
Frank-Wolfe methods (FW) have gained significant interest in the machine learning community due to its ability to efficiently solve large problems that admit a sparse structure (e.g. sparse vectors and low-rank matrices). However the performance of the existing FW method hinges on the quality of the linear approximation. This typically restricts FW to smooth functions for which the approximation quality, indicated by a global curvature measure, is reasonably good. In this paper, we propose a modified FW algorithm amenable to nonsmooth functions by optimizing for approximation quality over all affine approximations given a neighborhood of interest. We analyze theoretical properties of the proposed algorithm and demonstrate that it overcomes many issues associated with existing methods in the context of nonsmooth low-rank matrix estimation.

Projection Free Rank-Drop Steps

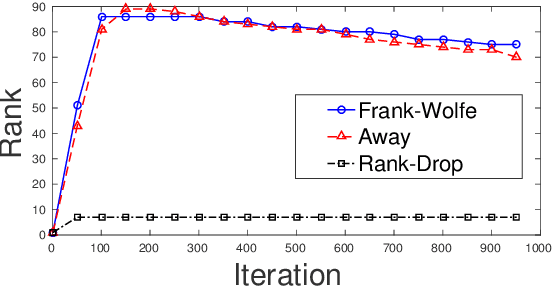
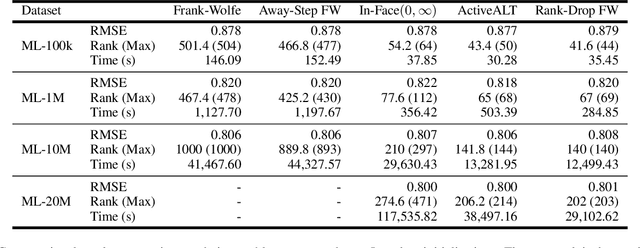
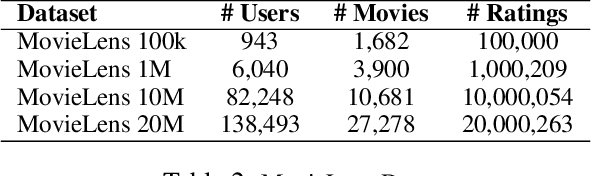
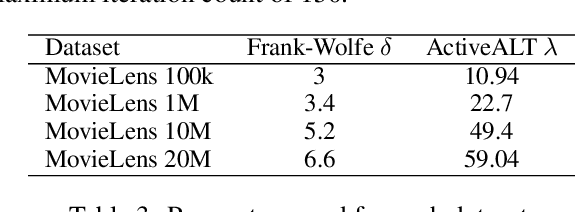
The Frank-Wolfe (FW) algorithm has been widely used in solving nuclear norm constrained problems, since it does not require projections. However, FW often yields high rank intermediate iterates, which can be very expensive in time and space costs for large problems. To address this issue, we propose a rank-drop method for nuclear norm constrained problems. The goal is to generate descent steps that lead to rank decreases, maintaining low-rank solutions throughout the algorithm. Moreover, the optimization problems are constrained to ensure that the rank-drop step is also feasible and can be readily incorporated into a projection-free minimization method, e.g., Frank-Wolfe. We demonstrate that by incorporating rank-drop steps into the Frank-Wolfe algorithm, the rank of the solution is greatly reduced compared to the original Frank-Wolfe or its common variants.