Projection Free Rank-Drop Steps
Paper and Code
Jul 04, 2017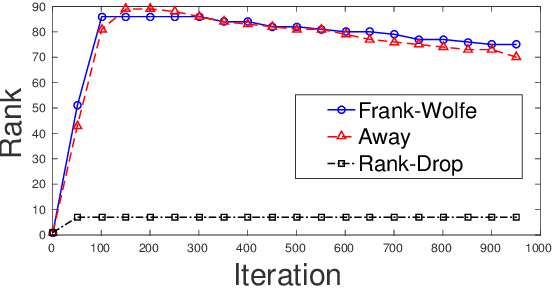
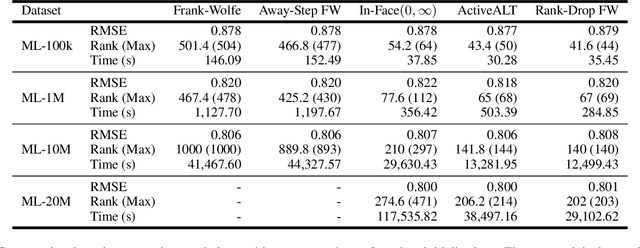
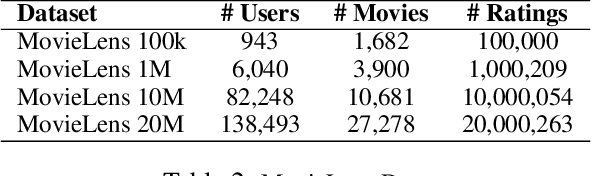
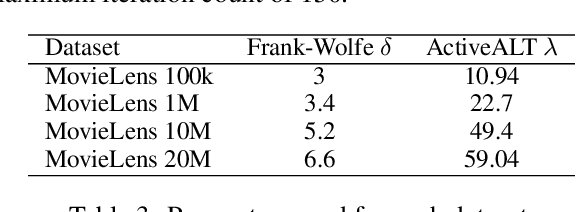
The Frank-Wolfe (FW) algorithm has been widely used in solving nuclear norm constrained problems, since it does not require projections. However, FW often yields high rank intermediate iterates, which can be very expensive in time and space costs for large problems. To address this issue, we propose a rank-drop method for nuclear norm constrained problems. The goal is to generate descent steps that lead to rank decreases, maintaining low-rank solutions throughout the algorithm. Moreover, the optimization problems are constrained to ensure that the rank-drop step is also feasible and can be readily incorporated into a projection-free minimization method, e.g., Frank-Wolfe. We demonstrate that by incorporating rank-drop steps into the Frank-Wolfe algorithm, the rank of the solution is greatly reduced compared to the original Frank-Wolfe or its common variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge