Forward Signal Propagation Learning

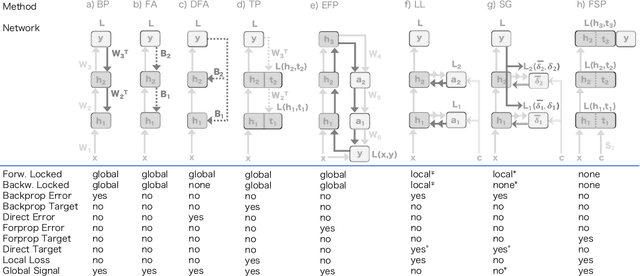
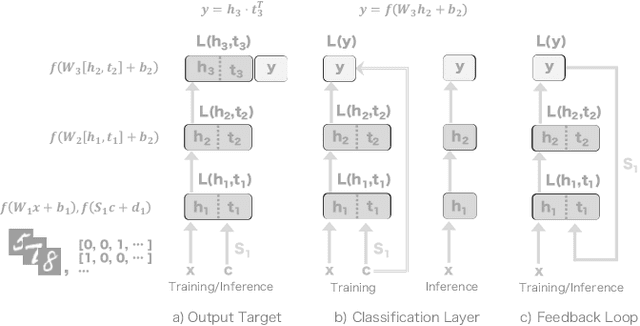
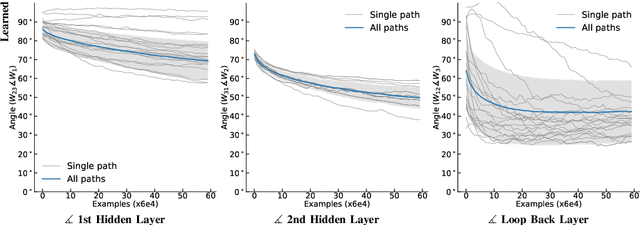
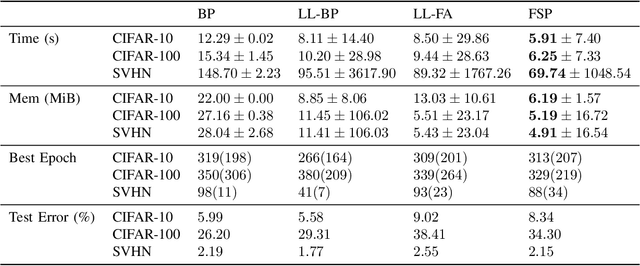
We propose a new learning algorithm for propagating a learning signal and updating neural network parameters via a forward pass, as an alternative to backpropagation. In forward signal propagation learning (sigprop), there is only the forward path for learning and inference, so there are no additional structural or computational constraints on learning, such as feedback connectivity, weight transport, or a backward pass, which exist under backpropagation. Sigprop enables global supervised learning with only a forward path. This is ideal for parallel training of layers or modules. In biology, this explains how neurons without feedback connections can still receive a global learning signal. In hardware, this provides an approach for global supervised learning without backward connectivity. Sigprop by design has better compatibility with models of learning in the brain and in hardware than backpropagation and alternative approaches to relaxing learning constraints. We also demonstrate that sigprop is more efficient in time and memory than they are. To further explain the behavior of sigprop, we provide evidence that sigprop provides useful learning signals in context to backpropagation. To further support relevance to biological and hardware learning, we use sigprop to train continuous time neural networks with Hebbian updates and train spiking neural networks without surrogate functions.

Error Forward-Propagation: Reusing Feedforward Connections to Propagate Errors in Deep Learning

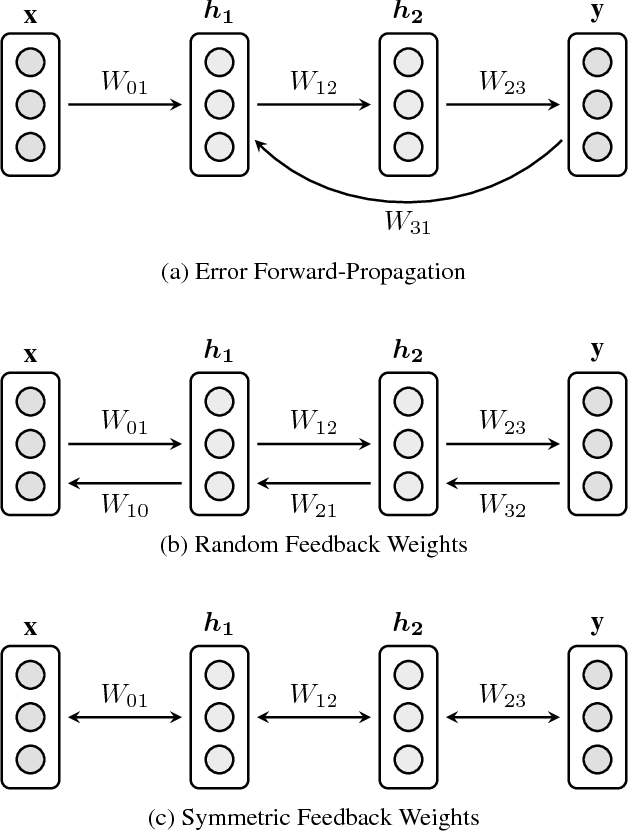
We introduce Error Forward-Propagation, a biologically plausible mechanism to propagate error feedback forward through the network. Architectural constraints on connectivity are virtually eliminated for error feedback in the brain; systematic backward connectivity is not used or needed to deliver error feedback. Feedback as a means of assigning credit to neurons earlier in the forward pathway for their contribution to the final output is thought to be used in learning in the brain. How the brain solves the credit assignment problem is unclear. In machine learning, error backpropagation is a highly successful mechanism for credit assignment in deep multilayered networks. Backpropagation requires symmetric reciprocal connectivity for every neuron. From a biological perspective, there is no evidence of such an architectural constraint, which makes backpropagation implausible for learning in the brain. This architectural constraint is reduced with the use of random feedback weights. Models using random feedback weights require backward connectivity patterns for every neuron, but avoid symmetric weights and reciprocal connections. In this paper, we practically remove this architectural constraint, requiring only a backward loop connection for effective error feedback. We propose reusing the forward connections to deliver the error feedback by feeding the outputs into the input receiving layer. This mechanism, Error Forward-Propagation, is a plausible basis for how error feedback occurs deep in the brain independent of and yet in support of the functionality underlying intricate network architectures. We show experimentally that recurrent neural networks with two and three hidden layers can be trained using Error Forward-Propagation on the MNIST and Fashion MNIST datasets, achieving $1.90\%$ and $11\%$ generalization errors respectively.

Using a Kernel Adatron for Object Classification with RCS Data

Rapid identification of object from radar cross section (RCS) signals is important for many space and military applications. This identification is a problem in pattern recognition which either neural networks or support vector machines should prove to be high-speed. Bayesian networks would also provide value but require significant preprocessing of the signals. In this paper, we describe the use of a support vector machine for object identification from synthesized RCS data. Our best results are from data fusion of X-band and S-band signals, where we obtained 99.4%, 95.3%, 100% and 95.6% correct identification for cylinders, frusta, spheres, and polygons, respectively. We also compare our results with a Bayesian approach and show that the SVM is three orders of magnitude faster, as measured by the number of floating point operations.