Edmund M. Clarke
Learning Probabilistic Systems from Tree Samples
Jul 21, 2012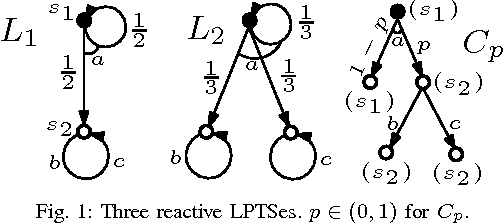
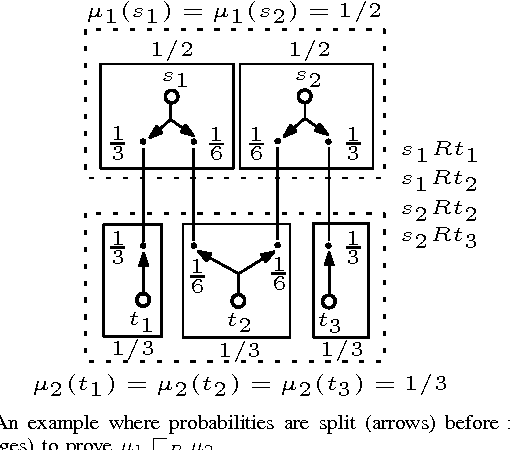
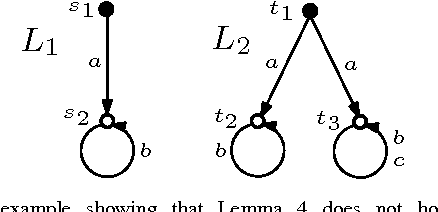
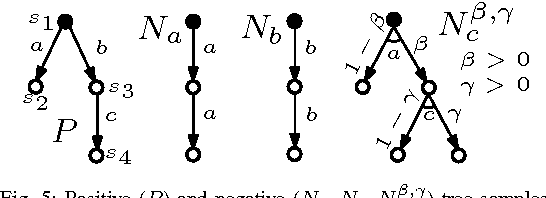
Abstract:We consider the problem of learning a non-deterministic probabilistic system consistent with a given finite set of positive and negative tree samples. Consistency is defined with respect to strong simulation conformance. We propose learning algorithms that use traditional and a new "stochastic" state-space partitioning, the latter resulting in the minimum number of states. We then use them to solve the problem of "active learning", that uses a knowledgeable teacher to generate samples as counterexamples to simulation equivalence queries. We show that the problem is undecidable in general, but that it becomes decidable under a suitable condition on the teacher which comes naturally from the way samples are generated from failed simulation checks. The latter problem is shown to be undecidable if we impose an additional condition on the learner to always conjecture a "minimum state" hypothesis. We therefore propose a semi-algorithm using stochastic partitions. Finally, we apply the proposed (semi-) algorithms to infer intermediate assumptions in an automated assume-guarantee verification framework for probabilistic systems.
* 14 pages, conference paper with full proofs
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge