Eden Abadi
Learning and Solving Regular Decision Processes
Mar 02, 2020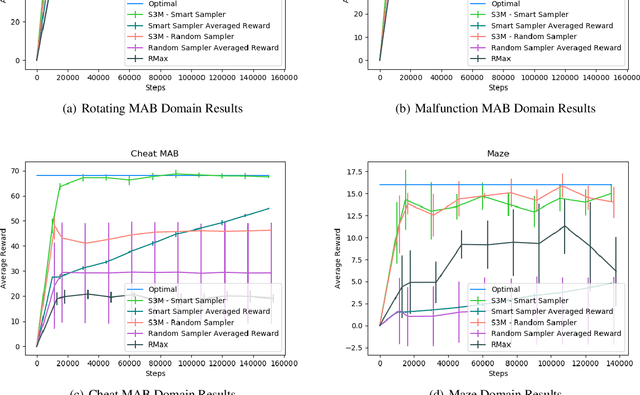
Abstract:Regular Decision Processes (RDPs) are a recently introduced model that extends MDPs with non-Markovian dynamics and rewards. The non-Markovian behavior is restricted to depend on regular properties of the history. These can be specified using regular expressions or formulas in linear dynamic logic over finite traces. Fully specified RDPs can be solved by compiling them into an appropriate MDP. Learning RDPs from data is a challenging problem that has yet to be addressed, on which we focus in this paper. Our approach rests on a new representation for RDPs using Mealy Machines that emit a distribution and an expected reward for each state-action pair. Building on this representation, we combine automata learning techniques with history clustering to learn such a Mealy machine and solve it by adapting MCTS to it. We empirically evaluate this approach, demonstrating its feasibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge