Resource Allocation Among Agents with MDP-Induced Preferences

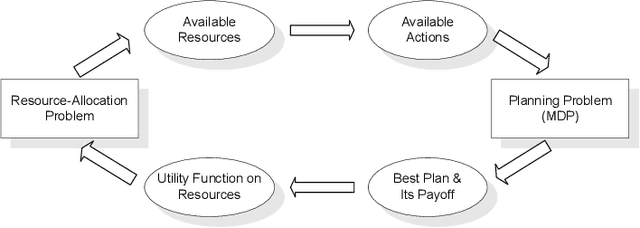
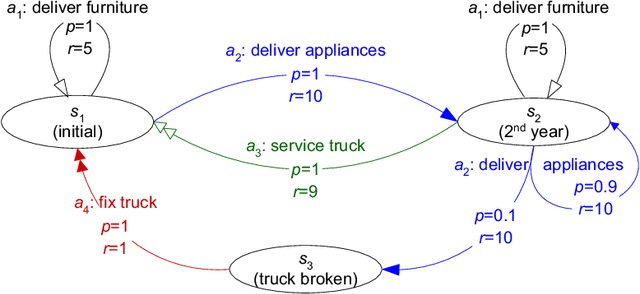
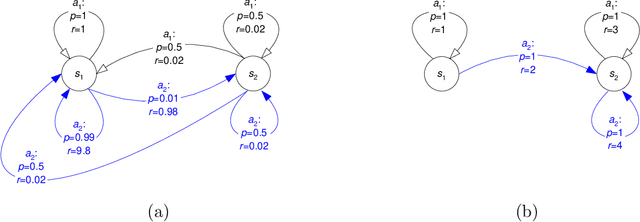
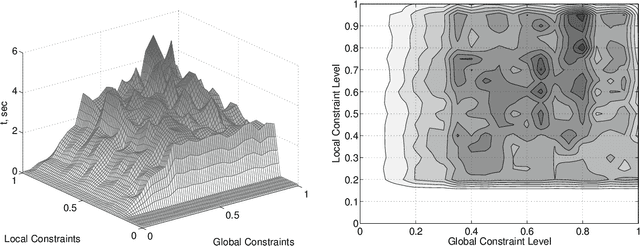
Allocating scarce resources among agents to maximize global utility is, in general, computationally challenging. We focus on problems where resources enable agents to execute actions in stochastic environments, modeled as Markov decision processes (MDPs), such that the value of a resource bundle is defined as the expected value of the optimal MDP policy realizable given these resources. We present an algorithm that simultaneously solves the resource-allocation and the policy-optimization problems. This allows us to avoid explicitly representing utilities over exponentially many resource bundles, leading to drastic (often exponential) reductions in computational complexity. We then use this algorithm in the context of self-interested agents to design a combinatorial auction for allocating resources. We empirically demonstrate the effectiveness of our approach by showing that it can, in minutes, optimally solve problems for which a straightforward combinatorial resource-allocation technique would require the agents to enumerate up to 2^100 resource bundles and the auctioneer to solve an NP-complete problem with an input of that size.

Use of Markov Chains to Design an Agent Bidding Strategy for Continuous Double Auctions

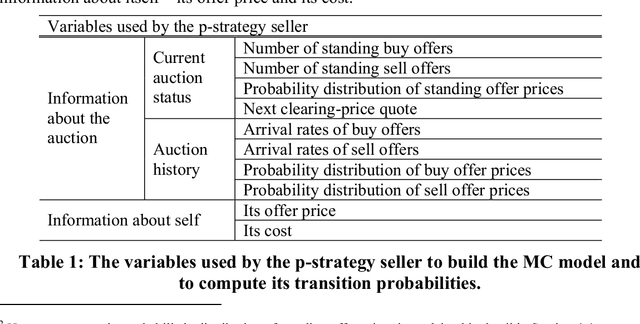
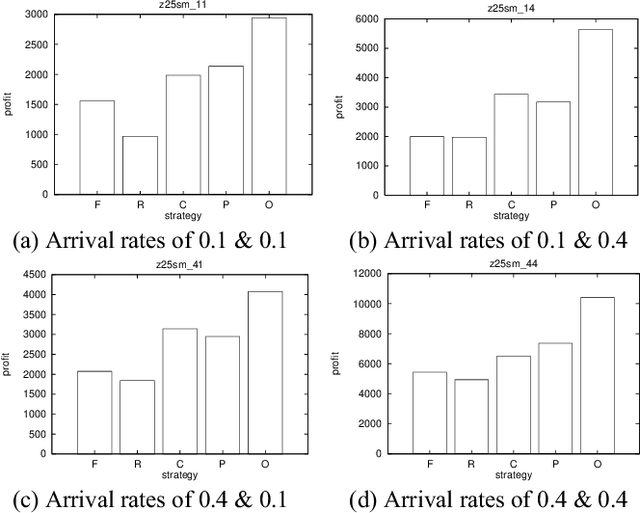
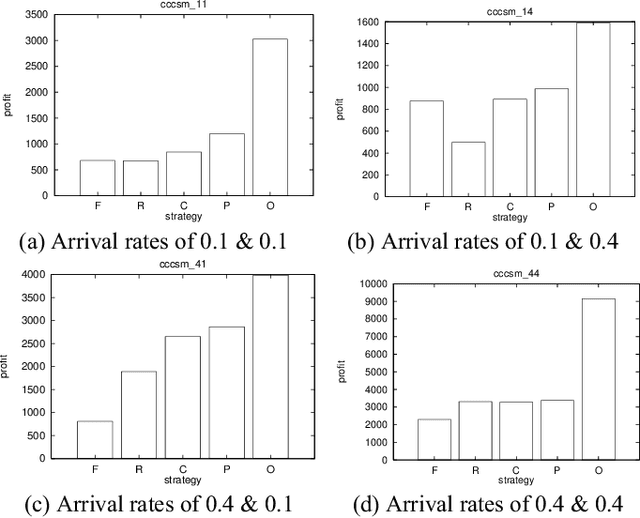
As computational agents are developed for increasingly complicated e-commerce applications, the complexity of the decisions they face demands advances in artificial intelligence techniques. For example, an agent representing a seller in an auction should try to maximize the seller's profit by reasoning about a variety of possibly uncertain pieces of information, such as the maximum prices various buyers might be willing to pay, the possible prices being offered by competing sellers, the rules by which the auction operates, the dynamic arrival and matching of offers to buy and sell, and so on. A naive application of multiagent reasoning techniques would require the seller's agent to explicitly model all of the other agents through an extended time horizon, rendering the problem intractable for many realistically-sized problems. We have instead devised a new strategy that an agent can use to determine its bid price based on a more tractable Markov chain model of the auction process. We have experimentally identified the conditions under which our new strategy works well, as well as how well it works in comparison to the optimal performance the agent could have achieved had it known the future. Our results show that our new strategy in general performs well, outperforming other tractable heuristic strategies in a majority of experiments, and is particularly effective in a 'seller?s market', where many buy offers are available.