Resource Allocation Among Agents with MDP-Induced Preferences
Paper and Code
Oct 12, 2011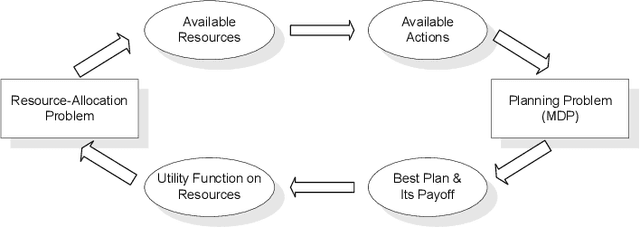
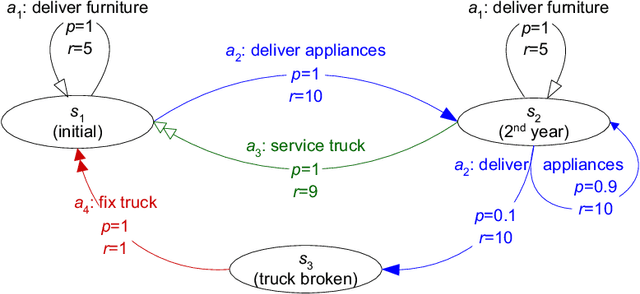
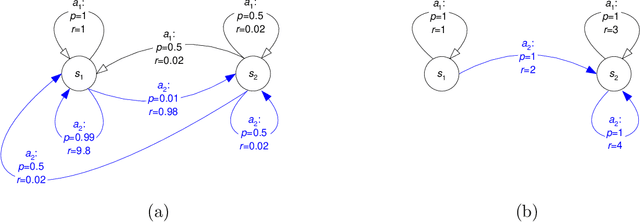
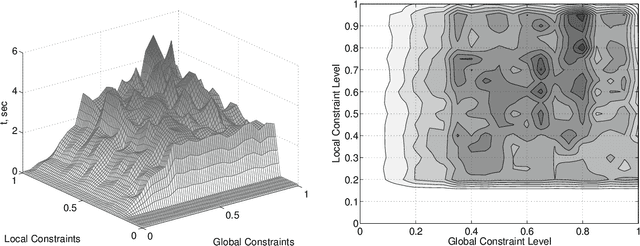
Allocating scarce resources among agents to maximize global utility is, in general, computationally challenging. We focus on problems where resources enable agents to execute actions in stochastic environments, modeled as Markov decision processes (MDPs), such that the value of a resource bundle is defined as the expected value of the optimal MDP policy realizable given these resources. We present an algorithm that simultaneously solves the resource-allocation and the policy-optimization problems. This allows us to avoid explicitly representing utilities over exponentially many resource bundles, leading to drastic (often exponential) reductions in computational complexity. We then use this algorithm in the context of self-interested agents to design a combinatorial auction for allocating resources. We empirically demonstrate the effectiveness of our approach by showing that it can, in minutes, optimally solve problems for which a straightforward combinatorial resource-allocation technique would require the agents to enumerate up to 2^100 resource bundles and the auctioneer to solve an NP-complete problem with an input of that size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge