Improving group robustness under noisy labels using predictive uncertainty

The standard empirical risk minimization (ERM) can underperform on certain minority groups (i.e., waterbirds in lands or landbirds in water) due to the spurious correlation between the input and its label. Several studies have improved the worst-group accuracy by focusing on the high-loss samples. The hypothesis behind this is that such high-loss samples are \textit{spurious-cue-free} (SCF) samples. However, these approaches can be problematic since the high-loss samples may also be samples with noisy labels in the real-world scenarios. To resolve this issue, we utilize the predictive uncertainty of a model to improve the worst-group accuracy under noisy labels. To motivate this, we theoretically show that the high-uncertainty samples are the SCF samples in the binary classification problem. This theoretical result implies that the predictive uncertainty is an adequate indicator to identify SCF samples in a noisy label setting. Motivated from this, we propose a novel ENtropy based Debiasing (END) framework that prevents models from learning the spurious cues while being robust to the noisy labels. In the END framework, we first train the \textit{identification model} to obtain the SCF samples from a training set using its predictive uncertainty. Then, another model is trained on the dataset augmented with an oversampled SCF set. The experimental results show that our END framework outperforms other strong baselines on several real-world benchmarks that consider both the noisy labels and the spurious-cues.

Improving evidential deep learning via multi-task learning

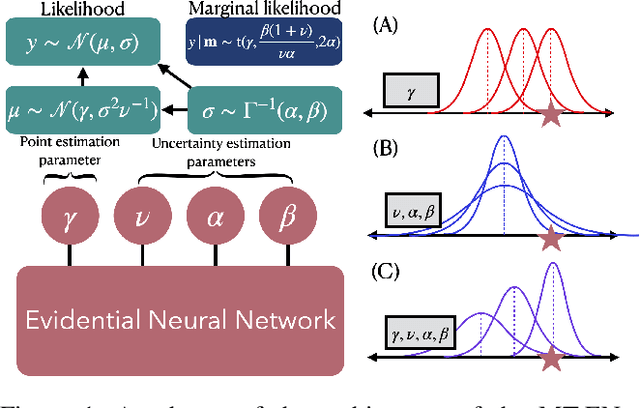
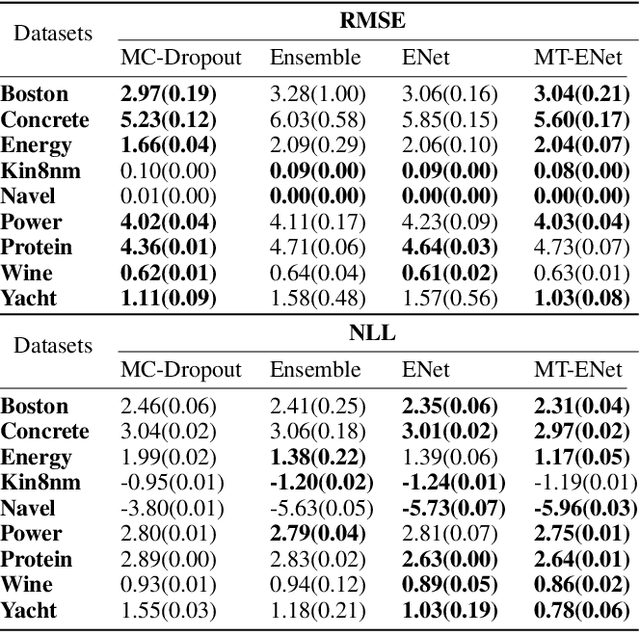
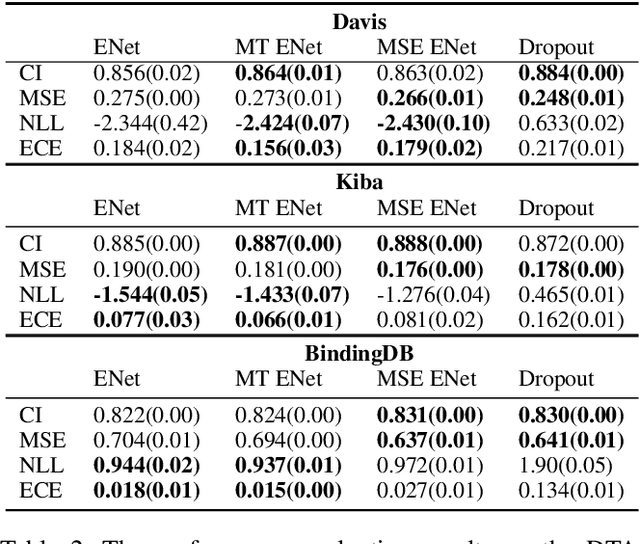
The Evidential regression network (ENet) estimates a continuous target and its predictive uncertainty without costly Bayesian model averaging. However, it is possible that the target is inaccurately predicted due to the gradient shrinkage problem of the original loss function of the ENet, the negative log marginal likelihood (NLL) loss. In this paper, the objective is to improve the prediction accuracy of the ENet while maintaining its efficient uncertainty estimation by resolving the gradient shrinkage problem. A multi-task learning (MTL) framework, referred to as MT-ENet, is proposed to accomplish this aim. In the MTL, we define the Lipschitz modified mean squared error (MSE) loss function as another loss and add it to the existing NLL loss. The Lipschitz modified MSE loss is designed to mitigate the gradient conflict with the NLL loss by dynamically adjusting its Lipschitz constant. By doing so, the Lipschitz MSE loss does not disturb the uncertainty estimation of the NLL loss. The MT-ENet enhances the predictive accuracy of the ENet without losing uncertainty estimation capability on the synthetic dataset and real-world benchmarks, including drug-target affinity (DTA) regression. Furthermore, the MT-ENet shows remarkable calibration and out-of-distribution detection capability on the DTA benchmarks.