Dominik Papies
School of Business and Economics, University of Tübingen
Double Machine Learning meets Panel Data -- Promises, Pitfalls, and Potential Solutions
Sep 02, 2024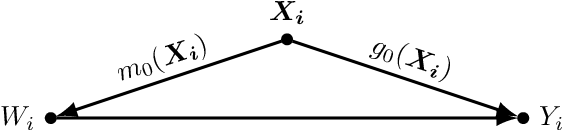
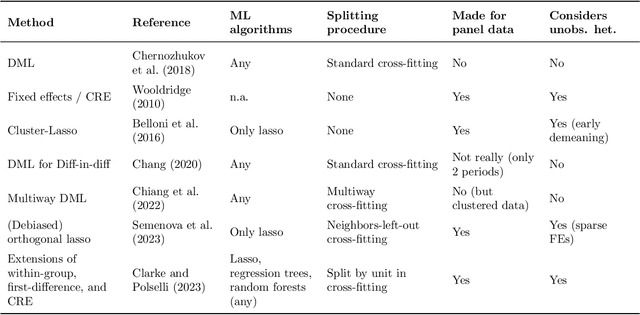
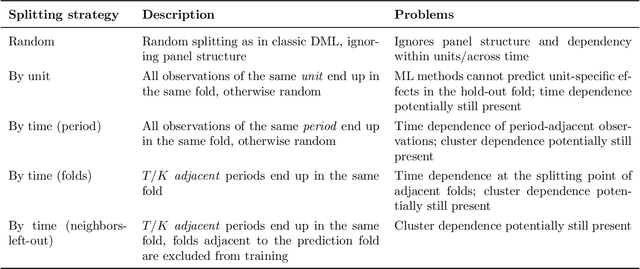
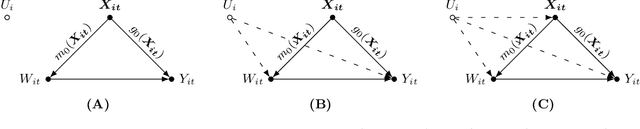
Abstract:Estimating causal effect using machine learning (ML) algorithms can help to relax functional form assumptions if used within appropriate frameworks. However, most of these frameworks assume settings with cross-sectional data, whereas researchers often have access to panel data, which in traditional methods helps to deal with unobserved heterogeneity between units. In this paper, we explore how we can adapt double/debiased machine learning (DML) (Chernozhukov et al., 2018) for panel data in the presence of unobserved heterogeneity. This adaptation is challenging because DML's cross-fitting procedure assumes independent data and the unobserved heterogeneity is not necessarily additively separable in settings with nonlinear observed confounding. We assess the performance of several intuitively appealing estimators in a variety of simulations. While we find violations of the cross-fitting assumptions to be largely inconsequential for the accuracy of the effect estimates, many of the considered methods fail to adequately account for the presence of unobserved heterogeneity. However, we find that using predictive models based on the correlated random effects approach (Mundlak, 1978) within DML leads to accurate coefficient estimates across settings, given a sample size that is large relative to the number of observed confounders. We also show that the influence of the unobserved heterogeneity on the observed confounders plays a significant role for the performance of most alternative methods.
Estimating Causal Effects with Double Machine Learning -- A Method Evaluation
Mar 21, 2024Abstract:The estimation of causal effects with observational data continues to be a very active research area. In recent years, researchers have developed new frameworks which use machine learning to relax classical assumptions necessary for the estimation of causal effects. In this paper, we review one of the most prominent methods - "double/debiased machine learning" (DML) - and empirically evaluate it by comparing its performance on simulated data relative to more traditional statistical methods, before applying it to real-world data. Our findings indicate that the application of a suitably flexible machine learning algorithm within DML improves the adjustment for various nonlinear confounding relationships. This advantage enables a departure from traditional functional form assumptions typically necessary in causal effect estimation. However, we demonstrate that the method continues to critically depend on standard assumptions about causal structure and identification. When estimating the effects of air pollution on housing prices in our application, we find that DML estimates are consistently larger than estimates of less flexible methods. From our overall results, we provide actionable recommendations for specific choices researchers must make when applying DML in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge