Heterogeneous Multi-Robot Graph Coverage with Proximity and Movement Constraints

Multi-Robot Coverage problems have been extensively studied in robotics, planning and multi-agent systems. In this work, we consider the coverage problem when there are constraints on the proximity (e.g., maximum distance between the agents, or a blue agent must be adjacent to a red agent) and the movement (e.g., terrain traversability and material load capacity) of the robots. Such constraints naturally arise in many real-world applications, e.g. in search-and-rescue and maintenance operations. Given such a setting, the goal is to compute a covering tour of the graph with a minimum number of steps, and that adheres to the proximity and movement constraints. For this problem, our contributions are four: (i) a formal formulation of the problem, (ii) an exact algorithm that is FPT in F, d and tw, the set of robot formations that encode the proximity constraints, the maximum nodes degree, and the tree-width of the graph, respectively, (iii) for the case that the graph is a tree: a PTAS approximation scheme, that given an approximation parameter epsilon, produces a tour that is within a epsilon times error(||F||, d) of the optimal one, and the computation runs in time poly(n) times h(1/epsilon,||F||). (iv) for the case that the graph is a tree, with $k=3$ robots, and the constraint is that all agents are connected: a PTAS scheme with multiplicative approximation error of 1+O(epsilon), independent of the maximal degree d.

Robust Solutions for Multi-Defender Stackelberg Security Games

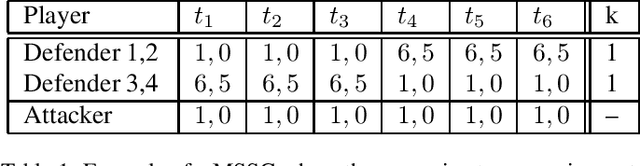
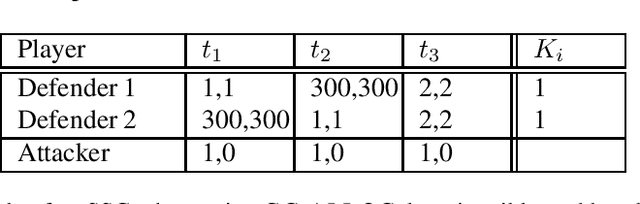
Multi-defender Stackelberg Security Games (MSSG) have recently gained increasing attention in the literature. However, the solutions offered to date are highly sensitive, wherein even small perturbations in the attacker's utility or slight uncertainties thereof can dramatically change the defenders' resulting payoffs and alter the equilibrium. In this paper, we introduce a robust model for MSSGs, which admits solutions that are resistant to small perturbations or uncertainties in the game's parameters. First, we formally define the notion of robustness, as well as the robust MSSG model. Then, for the non-cooperative setting, we prove the existence of a robust approximate equilibrium in any such game, and provide an efficient construction thereof. For the cooperative setting, we show that any such game admits a robust approximate alpha-core, provide an efficient construction thereof, and prove that stronger types of the core may be empty. Interestingly, the robust solutions can substantially increase the defenders' utilities over those of the non-robust ones.