Does Worst-Performing Agent Lead the Pack? Analyzing Agent Dynamics in Unified Distributed SGD

Distributed learning is essential to train machine learning algorithms across heterogeneous agents while maintaining data privacy. We conduct an asymptotic analysis of Unified Distributed SGD (UD-SGD), exploring a variety of communication patterns, including decentralized SGD and local SGD within Federated Learning (FL), as well as the increasing communication interval in the FL setting. In this study, we assess how different sampling strategies, such as i.i.d. sampling, shuffling, and Markovian sampling, affect the convergence speed of UD-SGD by considering the impact of agent dynamics on the limiting covariance matrix as described in the Central Limit Theorem (CLT). Our findings not only support existing theories on linear speedup and asymptotic network independence, but also theoretically and empirically show how efficient sampling strategies employed by individual agents contribute to overall convergence in UD-SGD. Simulations reveal that a few agents using highly efficient sampling can achieve or surpass the performance of the majority employing moderately improved strategies, providing new insights beyond traditional analyses focusing on the worst-performing agent.

Accelerating Distributed Stochastic Optimization via Self-Repellent Random Walks

We study a family of distributed stochastic optimization algorithms where gradients are sampled by a token traversing a network of agents in random-walk fashion. Typically, these random-walks are chosen to be Markov chains that asymptotically sample from a desired target distribution, and play a critical role in the convergence of the optimization iterates. In this paper, we take a novel approach by replacing the standard linear Markovian token by one which follows a nonlinear Markov chain - namely the Self-Repellent Radom Walk (SRRW). Defined for any given 'base' Markov chain, the SRRW, parameterized by a positive scalar {\alpha}, is less likely to transition to states that were highly visited in the past, thus the name. In the context of MCMC sampling on a graph, a recent breakthrough in Doshi et al. (2023) shows that the SRRW achieves O(1/{\alpha}) decrease in the asymptotic variance for sampling. We propose the use of a 'generalized' version of the SRRW to drive token algorithms for distributed stochastic optimization in the form of stochastic approximation, termed SA-SRRW. We prove that the optimization iterate errors of the resulting SA-SRRW converge to zero almost surely and prove a central limit theorem, deriving the explicit form of the resulting asymptotic covariance matrix corresponding to iterate errors. This asymptotic covariance is always smaller than that of an algorithm driven by the base Markov chain and decreases at rate O(1/{\alpha}^2) - the performance benefit of using SRRW thereby amplified in the stochastic optimization context. Empirical results support our theoretical findings.

Central Limit Theorem for Two-Timescale Stochastic Approximation with Markovian Noise: Theory and Applications

Two-timescale stochastic approximation (TTSA) is among the most general frameworks for iterative stochastic algorithms. This includes well-known stochastic optimization methods such as SGD variants and those designed for bilevel or minimax problems, as well as reinforcement learning like the family of gradient-based temporal difference (GTD) algorithms. In this paper, we conduct an in-depth asymptotic analysis of TTSA under controlled Markovian noise via central limit theorem (CLT), uncovering the coupled dynamics of TTSA influenced by the underlying Markov chain, which has not been addressed by previous CLT results of TTSA only with Martingale difference noise. Building upon our CLT, we expand its application horizon of efficient sampling strategies from vanilla SGD to a wider TTSA context in distributed learning, thus broadening the scope of Hu et al. (2022). In addition, we leverage our CLT result to deduce the statistical properties of GTD algorithms with nonlinear function approximation using Markovian samples and show their identical asymptotic performance, a perspective not evident from current finite-time bounds.

Self-Repellent Random Walks on General Graphs -- Achieving Minimal Sampling Variance via Nonlinear Markov Chains

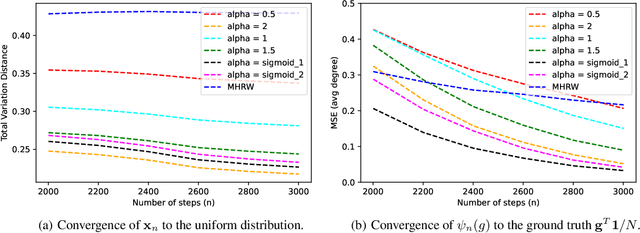
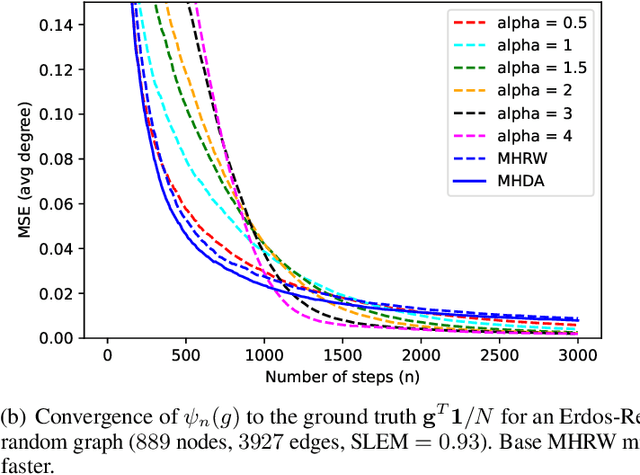
We consider random walks on discrete state spaces, such as general undirected graphs, where the random walkers are designed to approximate a target quantity over the network topology via sampling and neighborhood exploration in the form of Markov chain Monte Carlo (MCMC) procedures. Given any Markov chain corresponding to a target probability distribution, we design a self-repellent random walk (SRRW) which is less likely to transition to nodes that were highly visited in the past, and more likely to transition to seldom visited nodes. For a class of SRRWs parameterized by a positive real {\alpha}, we prove that the empirical distribution of the process converges almost surely to the the target (stationary) distribution of the underlying Markov chain kernel. We then provide a central limit theorem and derive the exact form of the arising asymptotic co-variance matrix, which allows us to show that the SRRW with a stronger repellence (larger {\alpha}) always achieves a smaller asymptotic covariance, in the sense of Loewner ordering of co-variance matrices. Especially for SRRW-driven MCMC algorithms, we show that the decrease in the asymptotic sampling variance is of the order O(1/{\alpha}), eventually going down to zero. Finally, we provide numerical simulations complimentary to our theoretical results, also empirically testing a version of SRRW with {\alpha} increasing in time to combine the benefits of smaller asymptotic variance due to large {\alpha}, with empirically observed faster mixing properties of SRRW with smaller {\alpha}.

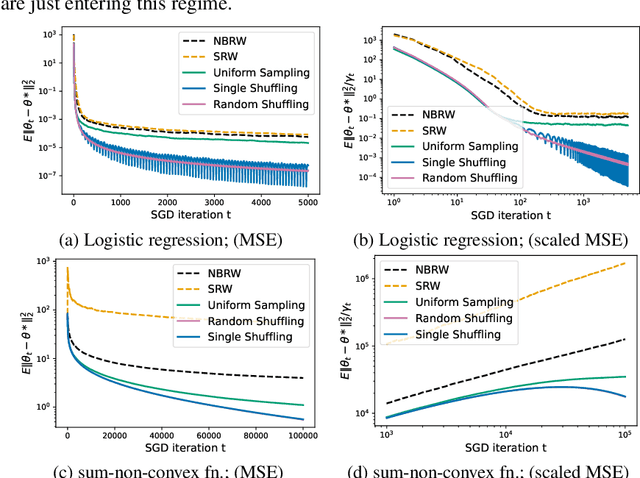
Efficiency Ordering of Stochastic Gradient Descent

We consider the stochastic gradient descent (SGD) algorithm driven by a general stochastic sequence, including i.i.d noise and random walk on an arbitrary graph, among others; and analyze it in the asymptotic sense. Specifically, we employ the notion of `efficiency ordering', a well-analyzed tool for comparing the performance of Markov Chain Monte Carlo (MCMC) samplers, for SGD algorithms in the form of Loewner ordering of covariance matrices associated with the scaled iterate errors in the long term. Using this ordering, we show that input sequences that are more efficient for MCMC sampling also lead to smaller covariance of the errors for SGD algorithms in the limit. This also suggests that an arbitrarily weighted MSE of SGD iterates in the limit becomes smaller when driven by more efficient chains. Our finding is of particular interest in applications such as decentralized optimization and swarm learning, where SGD is implemented in a random walk fashion on the underlying communication graph for cost issues and/or data privacy. We demonstrate how certain non-Markovian processes, for which typical mixing-time based non-asymptotic bounds are intractable, can outperform their Markovian counterparts in the sense of efficiency ordering for SGD. We show the utility of our method by applying it to gradient descent with shuffling and mini-batch gradient descent, reaffirming key results from existing literature under a unified framework. Empirically, we also observe efficiency ordering for variants of SGD such as accelerated SGD and Adam, open up the possibility of extending our notion of efficiency ordering to a broader family of stochastic optimization algorithms.