Dmytro Derkach
Local Shape Spectrum Analysis for 3D Facial Expression Recognition
May 19, 2017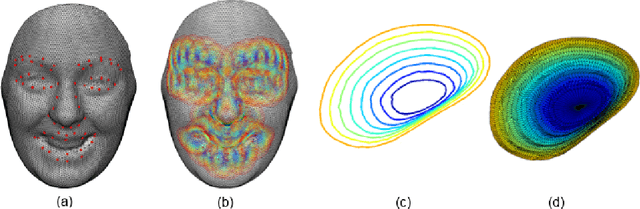
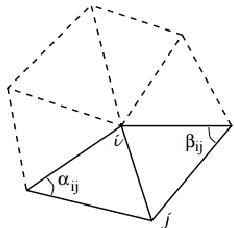
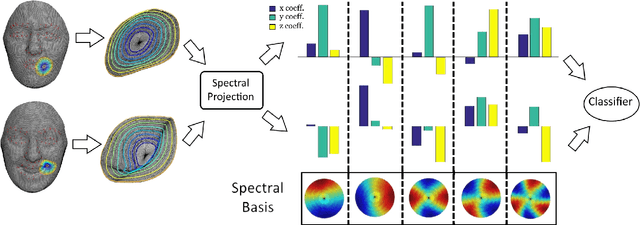

Abstract:We investigate the problem of facial expression recognition using 3D data. Building from one of the most successful frameworks for facial analysis using exclusively 3D geometry, we extend the analysis from a curve-based representation into a spectral representation, which allows a complete description of the underlying surface that can be further tuned to the desired level of detail. Spectral representations are based on the decomposition of the geometry in its spatial frequency components, much like a Fourier transform, which are related to intrinsic characteristics of the surface. In this work, we propose the use of Graph Laplacian Features (GLF), which results from the projection of local surface patches into a common basis obtained from the Graph Laplacian eigenspace. We test the proposed approach in the BU-3DFE database in terms of expressions and Action Units recognition. Our results confirm that the proposed GLF produces consistently higher recognition rates than the curves-based approach, thanks to a more complete description of the surface, while requiring a lower computational complexity. We also show that the GLF outperform the most popular alternative approach for spectral representation, Shape- DNA, which is based on the Laplace Beltrami Operator and cannot provide a stable basis that guarantee that the extracted signatures for the different patches are directly comparable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge