Improving hp-Variational Physics-Informed Neural Networks for Steady-State Convection-Dominated Problems

This paper proposes and studies two extensions of applying hp-variational physics-informed neural networks, more precisely the FastVPINNs framework, to convection-dominated convection-diffusion-reaction problems. First, a term in the spirit of a SUPG stabilization is included in the loss functional and a network architecture is proposed that predicts spatially varying stabilization parameters. Having observed that the selection of the indicator function in hard-constrained Dirichlet boundary conditions has a big impact on the accuracy of the computed solutions, the second novelty is the proposal of a network architecture that learns good parameters for a class of indicator functions. Numerical studies show that both proposals lead to noticeably more accurate results than approaches that can be found in the literature.

An efficient hp-Variational PINNs framework for incompressible Navier-Stokes equations

Physics-informed neural networks (PINNs) are able to solve partial differential equations (PDEs) by incorporating the residuals of the PDEs into their loss functions. Variational Physics-Informed Neural Networks (VPINNs) and hp-VPINNs use the variational form of the PDE residuals in their loss function. Although hp-VPINNs have shown promise over traditional PINNs, they suffer from higher training times and lack a framework capable of handling complex geometries, which limits their application to more complex PDEs. As such, hp-VPINNs have not been applied in solving the Navier-Stokes equations, amongst other problems in CFD, thus far. FastVPINNs was introduced to address these challenges by incorporating tensor-based loss computations, significantly improving the training efficiency. Moreover, by using the bilinear transformation, the FastVPINNs framework was able to solve PDEs on complex geometries. In the present work, we extend the FastVPINNs framework to vector-valued problems, with a particular focus on solving the incompressible Navier-Stokes equations for two-dimensional forward and inverse problems, including problems such as the lid-driven cavity flow, the Kovasznay flow, and flow past a backward-facing step for Reynolds numbers up to 200. Our results demonstrate a 2x improvement in training time while maintaining the same order of accuracy compared to PINNs algorithms documented in the literature. We further showcase the framework's efficiency in solving inverse problems for the incompressible Navier-Stokes equations by accurately identifying the Reynolds number of the underlying flow. Additionally, the framework's ability to handle complex geometries highlights its potential for broader applications in computational fluid dynamics. This implementation opens new avenues for research on hp-VPINNs, potentially extending their applicability to more complex problems.

FastVPINNs: Tensor-Driven Acceleration of VPINNs for Complex Geometries

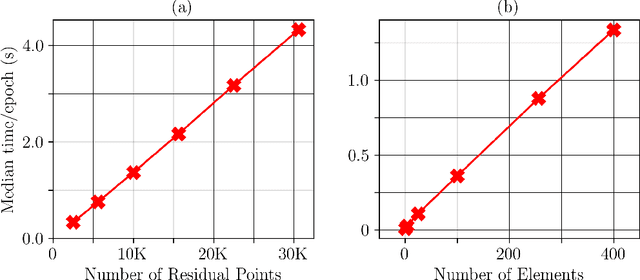
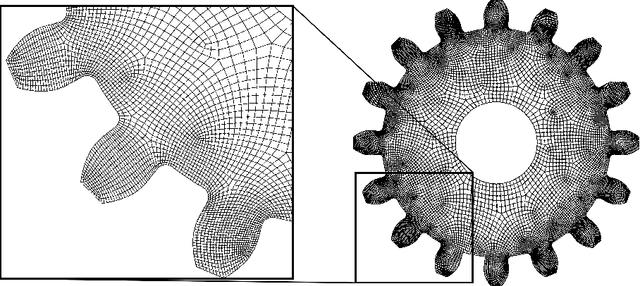
Variational Physics-Informed Neural Networks (VPINNs) utilize a variational loss function to solve partial differential equations, mirroring Finite Element Analysis techniques. Traditional hp-VPINNs, while effective for high-frequency problems, are computationally intensive and scale poorly with increasing element counts, limiting their use in complex geometries. This work introduces FastVPINNs, a tensor-based advancement that significantly reduces computational overhead and improves scalability. Using optimized tensor operations, FastVPINNs achieve a 100-fold reduction in the median training time per epoch compared to traditional hp-VPINNs. With proper choice of hyperparameters, FastVPINNs surpass conventional PINNs in both speed and accuracy, especially in problems with high-frequency solutions. Demonstrated effectiveness in solving inverse problems on complex domains underscores FastVPINNs' potential for widespread application in scientific and engineering challenges, opening new avenues for practical implementations in scientific machine learning.