Can I Trust My Fairness Metric? Assessing Fairness with Unlabeled Data and Bayesian Inference

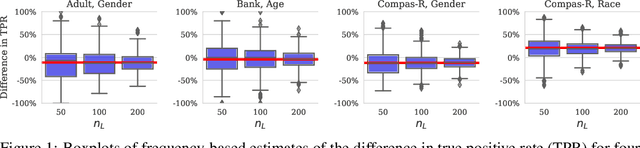
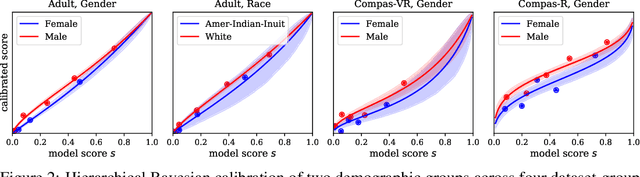
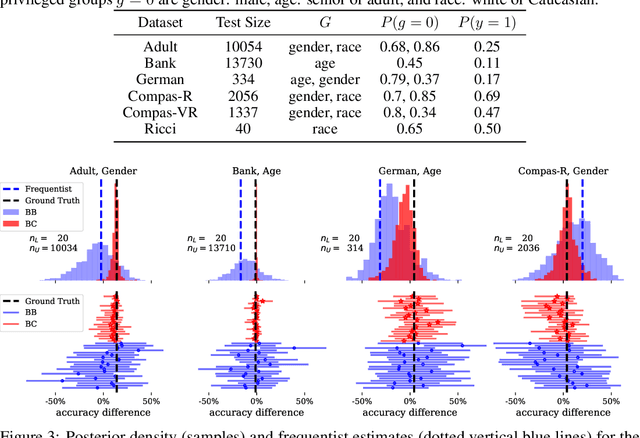
We investigate the problem of reliably assessing group fairness when labeled examples are few but unlabeled examples are plentiful. We propose a general Bayesian framework that can augment labeled data with unlabeled data to produce more accurate and lower-variance estimates compared to methods based on labeled data alone. Our approach estimates calibrated scores for unlabeled examples in each group using a hierarchical latent variable model conditioned on labeled examples. This in turn allows for inference of posterior distributions with associated notions of uncertainty for a variety of group fairness metrics. We demonstrate that our approach leads to significant and consistent reductions in estimation error across multiple well-known fairness datasets, sensitive attributes, and predictive models. The results show the benefits of using both unlabeled data and Bayesian inference in terms of assessing whether a prediction model is fair or not.

Active Bayesian Assessment for Black-Box Classifiers

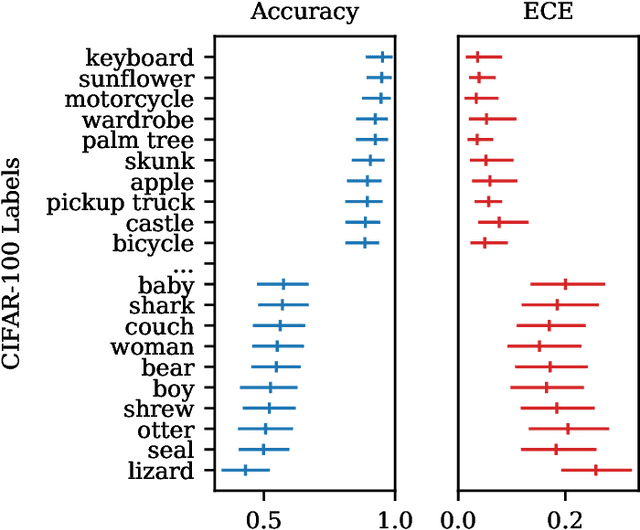
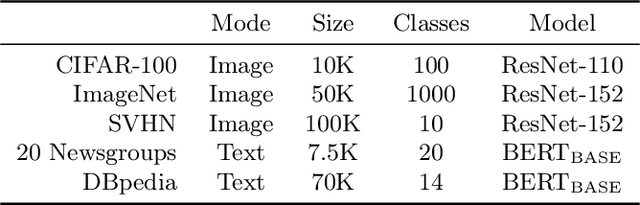
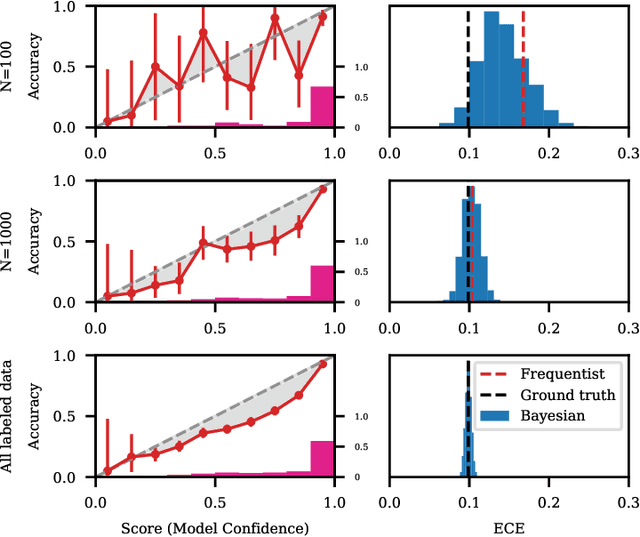
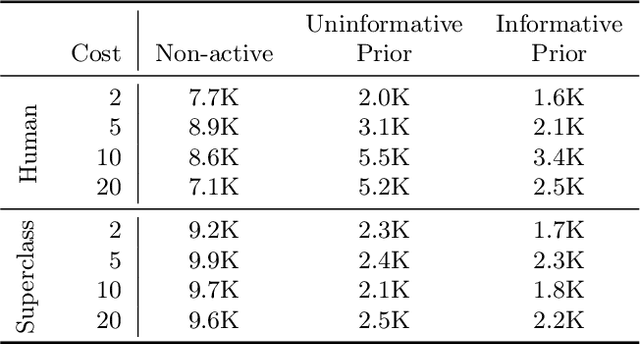
Recent advances in machine learning have led to increased deployment of black-box classifiers across a wide variety of applications. In many such situations there is a crucial need to assess the performance of these pre-trained models, for instance to ensure sufficient predictive accuracy, or that class probabilities are well-calibrated. Furthermore, since labeled data may be scarce or costly to collect, it is desirable for such assessment be performed in an efficient manner. In this paper, we introduce a Bayesian approach for model assessment that satisfies these desiderata. We develop inference strategies to quantify uncertainty for common assessment metrics (accuracy, misclassification cost, expected calibration error), and propose a framework for active assessment using this uncertainty to guide efficient selection of instances for labeling. We illustrate the benefits of our approach in experiments assessing the performance of modern neural classifiers (e.g., ResNet and BERT) on several standard image and text classification datasets.

Mondrian Processes for Flow Cytometry Analysis

Analysis of flow cytometry data is an essential tool for clinical diagnosis of hematological and immunological conditions. Current clinical workflows rely on a manual process called gating to classify cells into their canonical types. This dependence on human annotation limits the rate, reproducibility, and complexity of flow cytometry analysis. In this paper, we propose using Mondrian processes to perform automated gating by incorporating prior information of the kind used by gating technicians. The method segments cells into types via Bayesian nonparametric trees. Examining the posterior over trees allows for interpretable visualizations and uncertainty quantification - two vital qualities for implementation in clinical practice.