Dennis M. Kochmann
Deep learning-aided inverse design of porous metamaterials
Jul 23, 2025Abstract:The ultimate aim of the study is to explore the inverse design of porous metamaterials using a deep learning-based generative framework. Specifically, we develop a property-variational autoencoder (pVAE), a variational autoencoder (VAE) augmented with a regressor, to generate structured metamaterials with tailored hydraulic properties, such as porosity and permeability. While this work uses the lattice Boltzmann method (LBM) to generate intrinsic permeability tensor data for limited porous microstructures, a convolutional neural network (CNN) is trained using a bottom-up approach to predict effective hydraulic properties. This significantly reduces the computational cost compared to direct LBM simulations. The pVAE framework is trained on two datasets: a synthetic dataset of artificial porous microstructures and CT-scan images of volume elements from real open-cell foams. The encoder-decoder architecture of the VAE captures key microstructural features, mapping them into a compact and interpretable latent space for efficient structure-property exploration. The study provides a detailed analysis and interpretation of the latent space, demonstrating its role in structure-property mapping, interpolation, and inverse design. This approach facilitates the generation of new metamaterials with desired properties. The datasets and codes used in this study will be made open-access to support further research.
Physics-Informed Diffusion Models
Mar 21, 2024



Abstract:Generative models such as denoising diffusion models are quickly advancing their ability to approximate highly complex data distributions. They are also increasingly leveraged in scientific machine learning, where samples from the implied data distribution are expected to adhere to specific governing equations. We present a framework to inform denoising diffusion models on underlying constraints on such generated samples during model training. Our approach improves the alignment of the generated samples with the imposed constraints and significantly outperforms existing methods without affecting inference speed. Additionally, our findings suggest that incorporating such constraints during training provides a natural regularization against overfitting. Our framework is easy to implement and versatile in its applicability for imposing equality and inequality constraints as well as auxiliary optimization objectives.
GNN-Assisted Phase Space Integration with Application to Atomistics
Mar 20, 2023



Abstract:Overcoming the time scale limitations of atomistics can be achieved by switching from the state-space representation of Molecular Dynamics (MD) to a statistical-mechanics-based representation in phase space, where approximations such as maximum-entropy or Gaussian phase packets (GPP) evolve the atomistic ensemble in a time-coarsened fashion. In practice, this requires the computation of expensive high-dimensional integrals over all of phase space of an atomistic ensemble. This, in turn, is commonly accomplished efficiently by low-order numerical quadrature. We show that numerical quadrature in this context, unfortunately, comes with a set of inherent problems, which corrupt the accuracy of simulations -- especially when dealing with crystal lattices with imperfections. As a remedy, we demonstrate that Graph Neural Networks, trained on Monte-Carlo data, can serve as a replacement for commonly used numerical quadrature rules, overcoming their deficiencies and significantly improving the accuracy. This is showcased by three benchmarks: the thermal expansion of copper, the martensitic phase transition of iron, and the energy of grain boundaries. We illustrate the benefits of the proposed technique over classically used third- and fifth-order Gaussian quadrature, we highlight the impact on time-coarsened atomistic predictions, and we discuss the computational efficiency. The latter is of general importance when performing frequent evaluation of phase space or other high-dimensional integrals, which is why the proposed framework promises applications beyond the scope of atomistics.
Physics-Informed Neural Networks for Shell Structures
Jul 26, 2022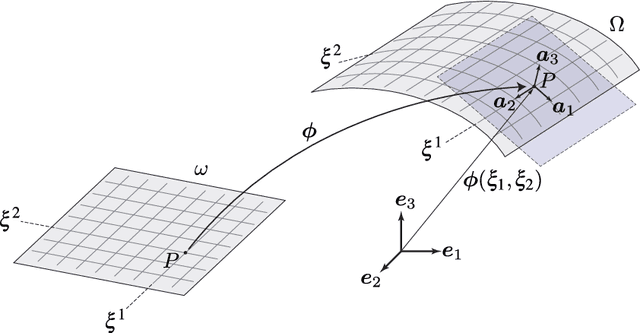
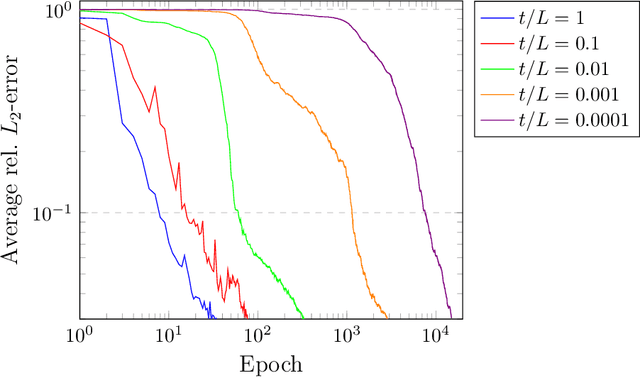
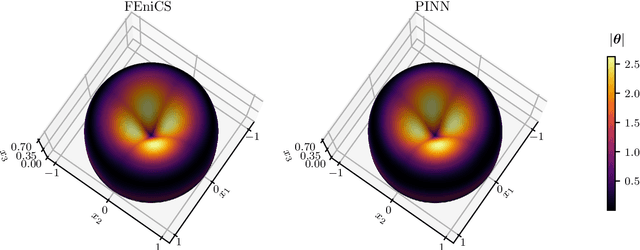
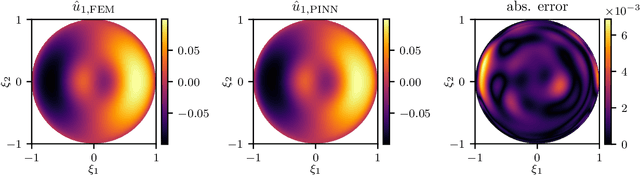
Abstract:The numerical modeling of thin shell structures is a challenge, which has been met by a variety of finite element (FE) and other formulations -- many of which give rise to new challenges, from complex implementations to artificial locking. As a potential alternative, we use machine learning and present a Physics-Informed Neural Network (PINN) to predict the small-strain response of arbitrarily curved shells. To this end, the shell midsurface is described by a chart, from which the mechanical fields are derived in a curvilinear coordinate frame by adopting Naghdi's shell theory. Unlike in typical PINN applications, the corresponding strong or weak form must therefore be solved in a non-Euclidean domain. We investigate the performance of the proposed PINN in three distinct scenarios, including the well-known Scordelis-Lo roof setting widely used to test FE shell elements against locking. Results show that the PINN can accurately identify the solution field in all three benchmarks if the equations are presented in their weak form, while it may fail to do so when using the strong form. In the thin-thickness limit, where classical methods are susceptible to locking, training time notably increases as the differences in scaling of the membrane, shear, and bending energies lead to adverse numerical stiffness in the gradient flow dynamics. Nevertheless, the PINN can accurately match the ground truth and performs well in the Scordelis-Lo roof benchmark, highlighting its potential for a drastically simplified alternative to designing locking-free shell FE formulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge