A Probabilistic Model of Action for Least-Commitment Planning with Information Gather

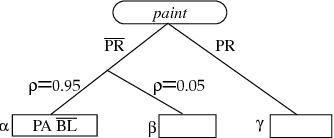
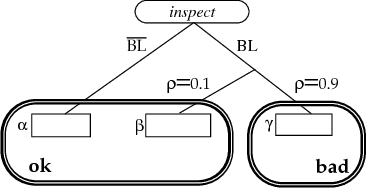
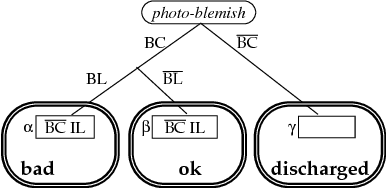
AI planning algorithms have addressed the problem of generating sequences of operators that achieve some input goal, usually assuming that the planning agent has perfect control over and information about the world. Relaxing these assumptions requires an extension to the action representation that allows reasoning both about the changes an action makes and the information it provides. This paper presents an action representation that extends the deterministic STRIPS model, allowing actions to have both causal and informational effects, both of which can be context dependent and noisy. We also demonstrate how a standard least-commitment planning algorithm can be extended to include informational actions and contingent execution.

Localized Partial Evaluation of Belief Networks

Most algorithms for propagating evidence through belief networks have been exact and exhaustive: they produce an exact (point-valued) marginal probability for every node in the network. Often, however, an application will not need information about every n ode in the network nor will it need exact probabilities. We present the localized partial evaluation (LPE) propagation algorithm, which computes interval bounds on the marginal probability of a specified query node by examining a subset of the nodes in the entire network. Conceptually, LPE ignores parts of the network that are "too far away" from the queried node to have much impact on its value. LPE has the "anytime" property of being able to produce better solutions (tighter intervals) given more time to consider more of the network.

Clustering Without (Thinking About) Triangulation

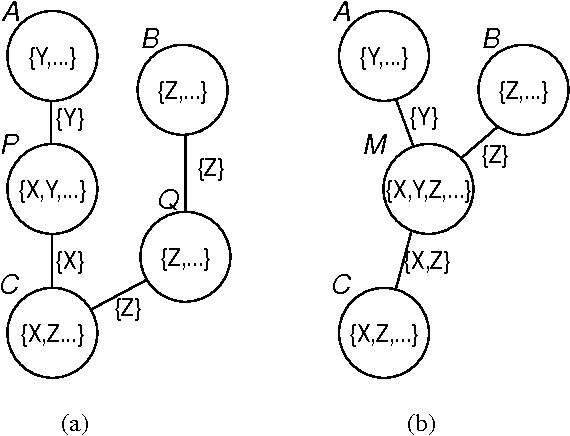
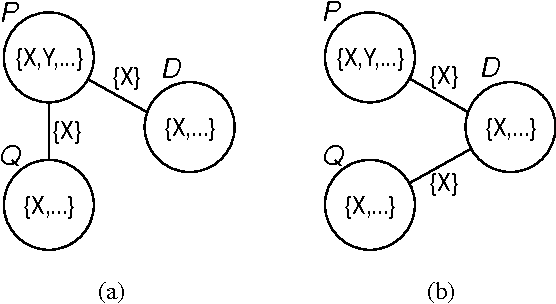
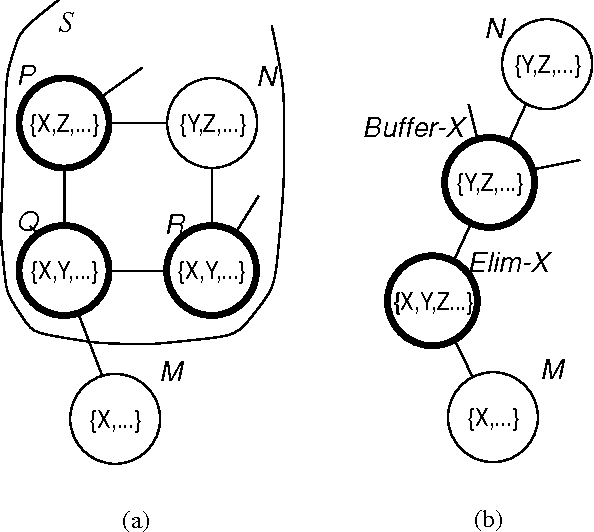
The undirected technique for evaluating belief networks [Jensen, et.al., 1990, Lauritzen and Spiegelhalter, 1988] requires clustering the nodes in the network into a junction tree. In the traditional view, the junction tree is constructed from the cliques of the moralized and triangulated belief network: triangulation is taken to be the primitive concept, the goal towards which any clustering algorithm (e.g. node elimination) is directed. In this paper, we present an alternative conception of clustering, in which clusters and the junction tree property play the role of primitives: given a graph (not a tree) of clusters which obey (a modified version of) the junction tree property, we transform this graph until we have obtained a tree. There are several advantages to this approach: it is much clearer and easier to understand, which is important for humans who are constructing belief networks; it admits a wider range of heuristics which may enable more efficient or superior clustering algorithms; and it serves as the natural basis for an incremental clustering scheme, which we describe.