A Bayesian framework for the analog reconstruction of kymographs from fluorescence microscopy data

Kymographs are widely used to represent and anal- yse spatio-temporal dynamics of fluorescence markers along curvilinear biological compartments. These objects have a sin- gular geometry, thus kymograph reconstruction is inherently an analog image processing task. However, the existing approaches are essentially digital: the kymograph photometry is sampled directly from the time-lapse images. As a result, such kymographs rely on raw image data that suffer from the degradations entailed by the image formation process and the spatio-temporal resolution of the imaging setup. In this work, we address these limitations and introduce a well-grounded Bayesian framework for the analog reconstruction of kymographs. To handle the movement of the object, we introduce an intrinsic description of kymographs using differential geometry: a kymograph is a photometry defined on a parameter space that is embedded in physical space by a time-varying map that follows the object geometry. We model the kymograph photometry as a L\'evy innovation process, a flexible class of non-parametric signal priors. We account for the image formation process using the virtual microscope framework. We formulate a computationally tractable representation of the associated maximum a posteriori problem and solve it using a class of efficient and modular algorithms based on the alternating split Bregman. We assess the performance of our Bayesian framework on synthetic data and apply it to reconstruct the fluorescence dynamics along microtubules in vivo in the budding yeast S. cerevisiae. We demonstrate that our framework allows revealing patterns from single time-lapse data that are invisible on standard digital kymographs.

Modelling Point Spread Function in Fluorescence Microscopy with a Sparse Combination of Gaussian Mixture: Trade-off between Accuracy and Efficiency

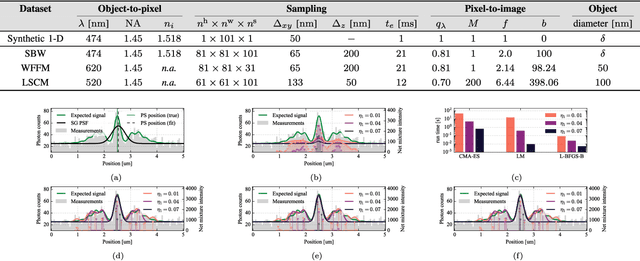
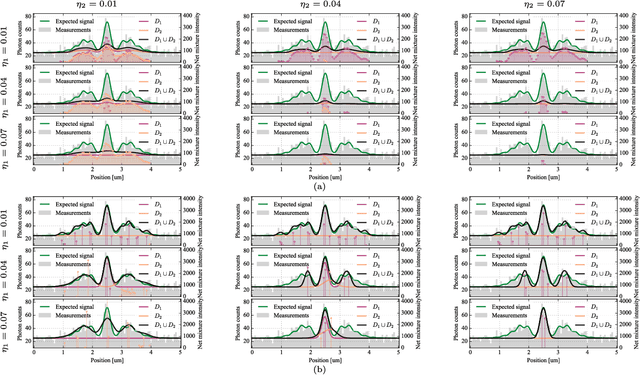
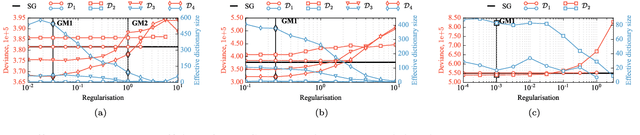
Deblurring is a fundamental inverse problem in bioimaging. It requires modelling the point spread function (PSF), which captures the optical distortions entailed by the image formation process. The PSF limits the spatial resolution attainable for a given microscope. However, recent applications require a higher resolution, and have prompted the development of super-resolution techniques to achieve sub-pixel accuracy. This requirement restricts the class of suitable PSF models to analog ones. In addition, deblurring is computationally intensive, hence further requiring computationally efficient models. A custom candidate fitting both requirements is the Gaussian model. However, this model cannot capture the rich tail structures found in both theoretical and empirical PSFs. In this paper, we aim at improving the reconstruction accuracy beyond the Gaussian model, while preserving its computational efficiency. We introduce a new class of analog PSF models based on Gaussian mixtures. The number of Gaussian kernels controls both the modelling accuracy and the computational efficiency of the model: the lower the number of kernels, the lower accuracy and the higher efficiency. To explore the accuracy--efficiency trade-off, we propose a variational formulation of the PSF calibration problem, where a convex sparsity-inducing penalty on the number of Gaussian kernels allows trading accuracy for efficiency. We derive an efficient algorithm based on a fully-split formulation of alternating split Bregman. We assess our framework on synthetic and real data and demonstrate a better reconstruction accuracy in both geometry and photometry in point source localisation---a fundamental inverse problem in fluorescence microscopy.