Modelling Point Spread Function in Fluorescence Microscopy with a Sparse Combination of Gaussian Mixture: Trade-off between Accuracy and Efficiency

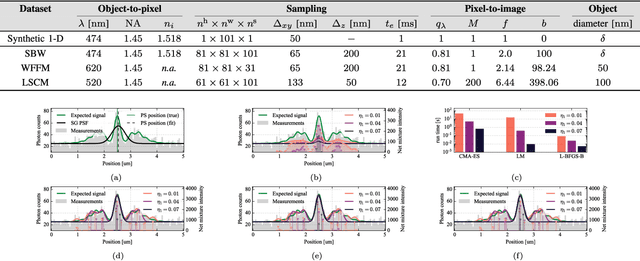
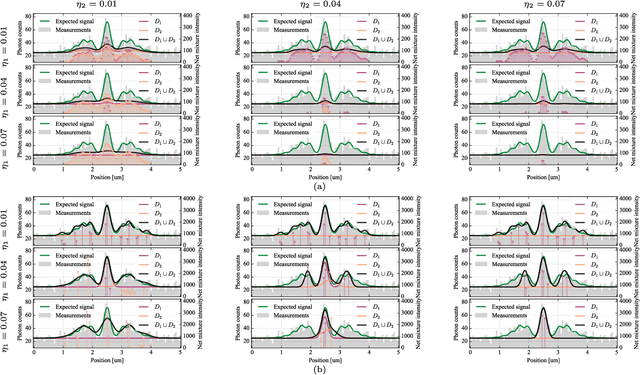
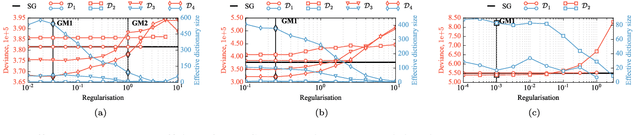
Deblurring is a fundamental inverse problem in bioimaging. It requires modelling the point spread function (PSF), which captures the optical distortions entailed by the image formation process. The PSF limits the spatial resolution attainable for a given microscope. However, recent applications require a higher resolution, and have prompted the development of super-resolution techniques to achieve sub-pixel accuracy. This requirement restricts the class of suitable PSF models to analog ones. In addition, deblurring is computationally intensive, hence further requiring computationally efficient models. A custom candidate fitting both requirements is the Gaussian model. However, this model cannot capture the rich tail structures found in both theoretical and empirical PSFs. In this paper, we aim at improving the reconstruction accuracy beyond the Gaussian model, while preserving its computational efficiency. We introduce a new class of analog PSF models based on Gaussian mixtures. The number of Gaussian kernels controls both the modelling accuracy and the computational efficiency of the model: the lower the number of kernels, the lower accuracy and the higher efficiency. To explore the accuracy--efficiency trade-off, we propose a variational formulation of the PSF calibration problem, where a convex sparsity-inducing penalty on the number of Gaussian kernels allows trading accuracy for efficiency. We derive an efficient algorithm based on a fully-split formulation of alternating split Bregman. We assess our framework on synthetic and real data and demonstrate a better reconstruction accuracy in both geometry and photometry in point source localisation---a fundamental inverse problem in fluorescence microscopy.