Joint Sampling Frequency Offset Estimation and Compensation Based on the Farrow Structure

This paper introduces a sampling frequency offset (SFO) estimation method based on the Farrow structure, which is typically utilized for the SFO compensation and thereby enables a reduction of the implementation complexity of the SFO estimation. The proposed method is implemented in the time domain and works for arbitrary bandlimited signals, thus with no additional constraints on the waveform structure. Moreover, it can operate on only the real or imaginary part of a complex signal, which further reduces the estimation complexity. Furthermore, the proposed method can simultaneously estimate the SFO and additional sampling time offset (STO) and it is insensitive to other synchronization errors, like carrier frequency offset. Both the derivations of the proposed method and its implementation are presented, and through simulation examples, it is demonstrated that it can accurately estimate both SFO and STO for different types of bandlimited signals.

Digital Linearizer Based on 1-Bit Quantizations

This paper introduces a novel low-complexity memoryless linearizer for suppression of distortion in analog frontends. It is based on our recently introduced linearizer which is inspired by neural networks, but with orders-of-magnitude lower complexity than conventional neural-networks considered in this context, and it can also outperform the conventional parallel memoryless Hammerstein linearizer. Further, it can be designed through matrix inversion and thereby the costly and time consuming numerical optimization traditionally used when training neural networks is avoided. The linearizer proposed in this paper is different in that it uses 1-bit quantizations as nonlinear activation functions and different bias values. These features enable a look-up table implementation which eliminates all but one of the multiplications and additions required for the linearization. Extensive simulations and comparisons are included in the paper, for distorted multi-tone signals and bandpass filtered white noise, which demonstrate the efficacy of the proposed linearizer.

Low-Complexity Frequency-Dependent Linearizers Based on Parallel Bias-Modulus and Bias-ReLU Operations

This paper introduces low-complexity frequency-dependent (memory) linearizers designed to suppress nonlinear distortion in analog-to-digital interfaces. Two different linearizers are considered, based on nonlinearity models which correspond to sampling before and after the nonlinearity operations, respectively. The proposed linearizers are inspired by convolutional neural networks but have an order-of-magnitude lower implementation complexity compared to existing neural-network-based linearizer schemes. The proposed linearizers can also outperform the traditional parallel Hammerstein (as well as Wiener) linearizers even when the nonlinearities have been generated through a Hammerstein model. Further, a design procedure is proposed in which the linearizer parameters are obtained through matrix inversion. This eliminates the need for costly and time-consuming iterative nonconvex optimization which is traditionally associated with neural network training. The design effectively handles a wide range of wideband multi-tone signals and filtered white noise. Examples demonstrate significant signal-to-noise-and-distortion ratio (SNDR) improvements of some $20$--$30$ dB, as well as a lower implementation complexity than the Hammerstein linearizers.

Order Estimation of Linear-Phase FIR Filters for DAC Equalization in Multiple Nyquist Bands

This letter considers the design of linear-phase finite-length impulse response (FIR) filters for equalization of the frequency responses of digital-to-analog converters (DACs). The letter derives estimates for the filter orders required, as functions of the bandwidth and equalization accuracy, for four DAC pulses that are used in DACs in multiple Nyquist bands. The estimates are derived through a large set of minimax-optimal equalizers and the use of symbolic regression followed by minimax-optimal curve fitting for further enhancement. Design examples included demonstrate the accuracy of the proposed estimates. In addition, the letter discusses the appropriateness of the four types of linear-phase FIR filters, for the different equalizer cases, as well as the corresponding properties of the equalized systems.

Low-Complexity Memoryless Linearizer for Analog-to-Digital Interfaces

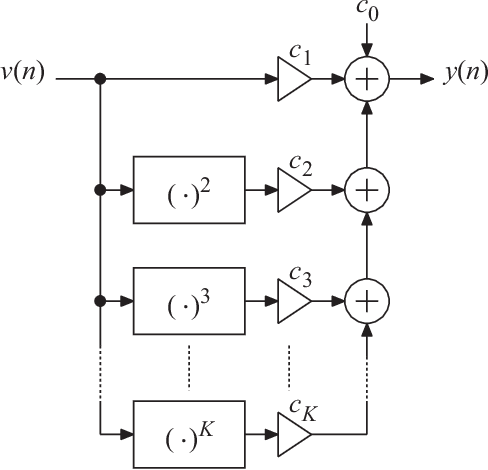
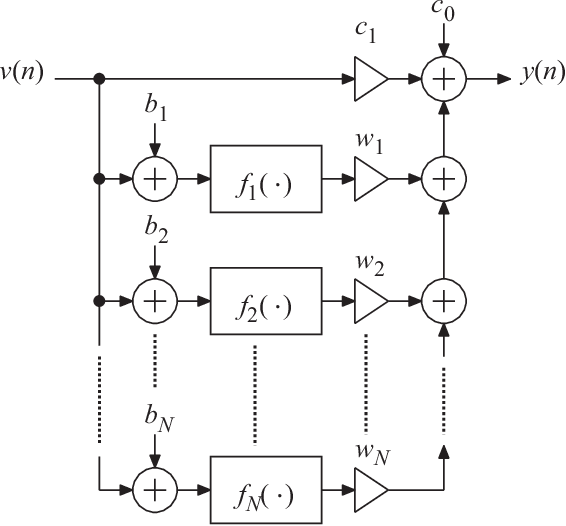
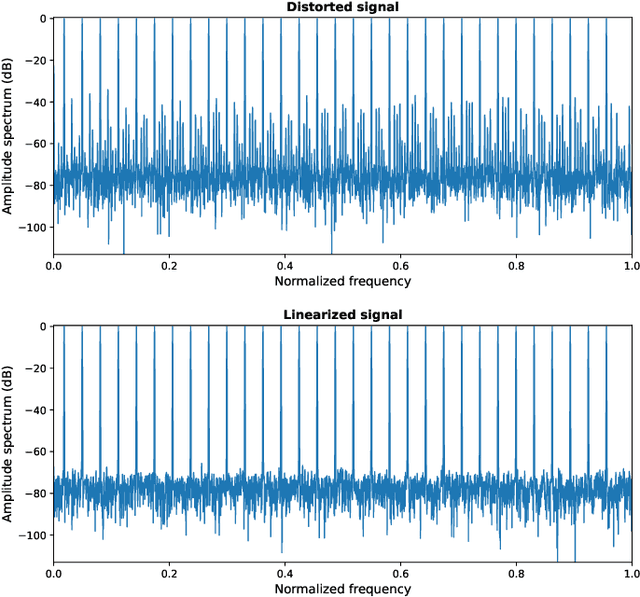
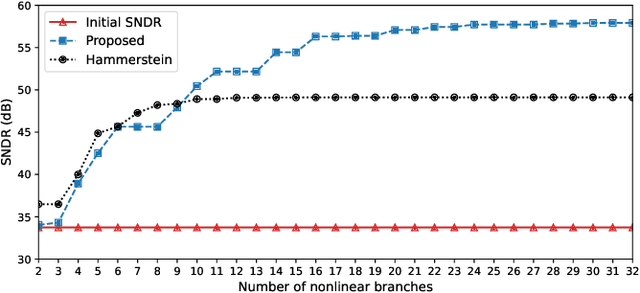
This paper introduces a low-complexity memoryless linearizer for suppression of distortion in analog-to-digital interfaces. It is inspired by neural networks, but has a substantially lower complexity than the neural-network schemes that have appeared earlier in the literature in this context. The paper demonstrates that the proposed linearizer can outperform the conventional parallel memoryless Hammerstein linearizer even when the nonlinearities have been generated through a memoryless polynomial model. Further, a design procedure is proposed in which the linearizer parameters are obtained through matrix inversion. Thereby, the costly and time consuming numerical optimization that is traditionally used when training neural networks is eliminated. Moreover, the design and evaluation incorporate a large set of multi-tone signals covering the first Nyquist band. Simulations show signal-to-noise-and-distortion ratio (SNDR) improvements of some 25 dB for multi-tone signals that correspond to the quadrature parts of OFDM signals with QPSK modulation.