Defang Li
Random Euler Complex-Valued Nonlinear Filters
Jan 02, 2018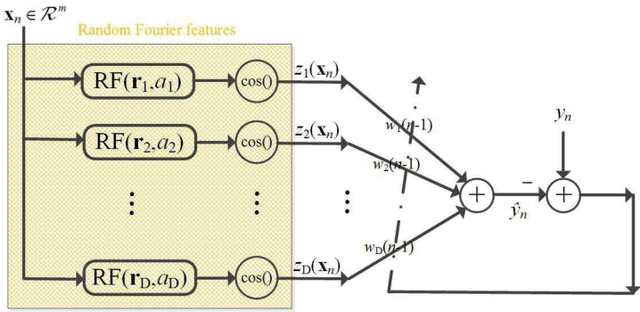
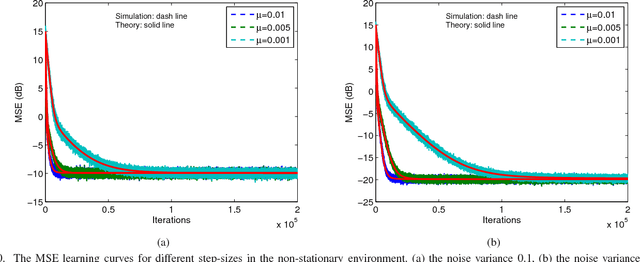
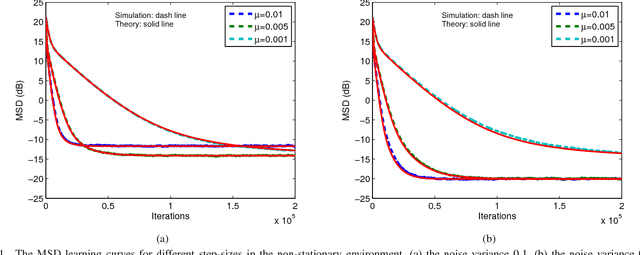
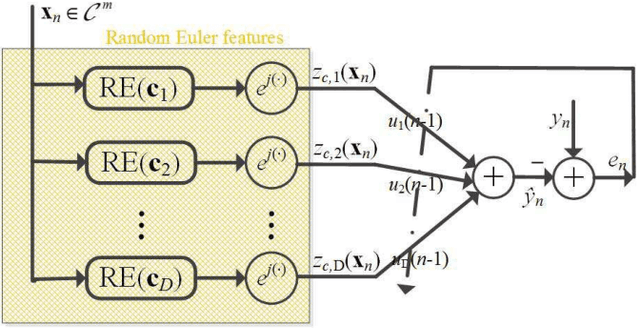
Abstract:Over the last decade, both the neural network and kernel adaptive filter have successfully been used for nonlinear signal processing. However, they suffer from high computational cost caused by their complex/growing network structures. In this paper, we propose two random Euler filters for complex-valued nonlinear filtering problem, i.e., linear random Euler complex-valued filter (LRECF) and its widely-linear version (WLRECF), which possess a simple and fixed network structure. The transient and steady-state performances are studied in a non-stationary environment. The analytical minimum mean square error (MSE) and optimum step-size are derived. Finally, numerical simulations on complex-valued nonlinear system identification and nonlinear channel equalization are presented to show the effectiveness of the proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge