Symmetry Adapted Residual Neural Network Diabatization: Conical Intersections in Aniline Photodissociation

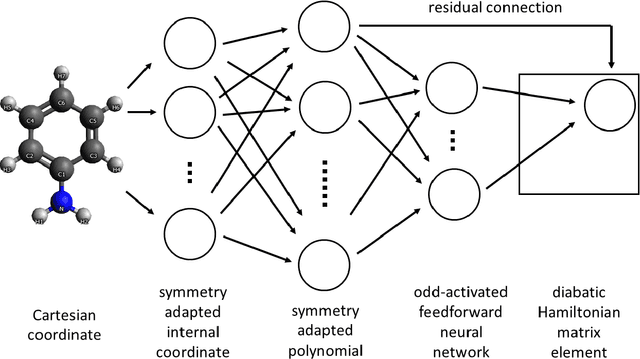
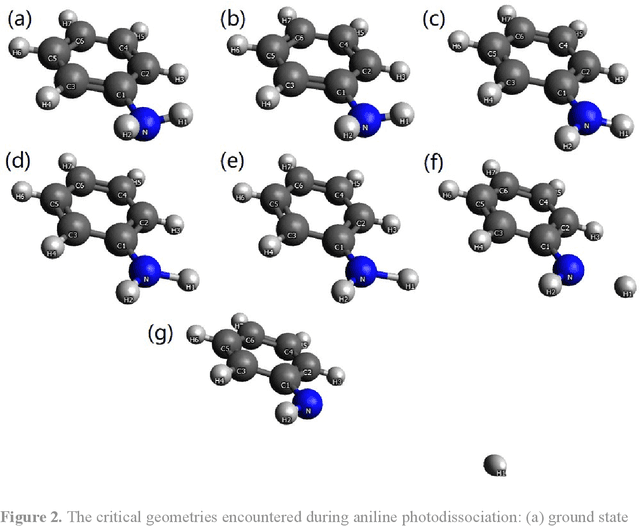
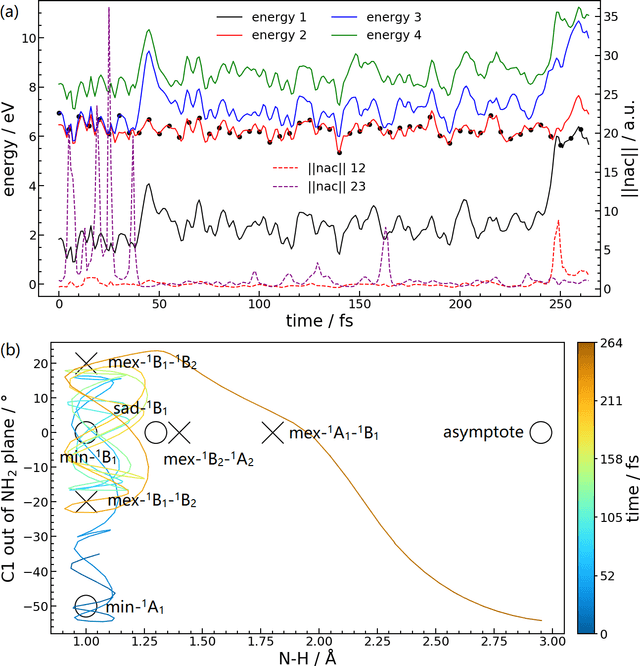
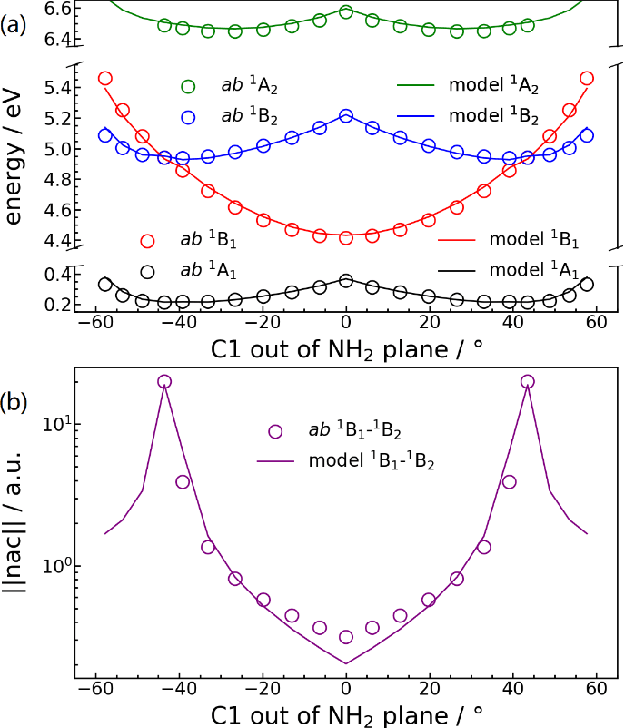
We present a symmetry adapted residual neural network (SAResNet) diabatization method to construct quasi-diabatic Hamiltonians that accurately represent ab initio adiabatic energies, energy gradients, and nonadiabatic couplings for moderate sized systems. Our symmetry adapted neural network inherits from the pioneering symmetry adapted polynomial and fundamental invariant neural network diabatization methods to exploit the power of neural network along with the transparent symmetry adaptation of polynomial for both symmetric and asymmetric irreducible representations. In addition, our symmetry adaptation provides a unified framework for symmetry adapted polynomial and symmetry adapted neural network, enabling the adoption of the residual neural network architecture, which is a powerful descendant of the pioneering feedforward neural network. Our SAResNet is applied to construct the full 36-dimensional coupled diabatic potential energy surfaces for aniline N-H bond photodissociation, with 2,269 data points and 32,640 trainable parameters and 190 cm-1 root mean square deviation in energy. In addition to the experimentally observed {\pi}{\pi}* and {\pi}Rydberg/{\pi}{\sigma}* states, a higher state (HOMO - 1 {\pi} to Rydberg/{\sigma}* excitation) is found to introduce an induced geometric phase effect thus indirectly participate in the photodissociation process.