Autonomous Subsea Cable Search and Tracking with Graph-Optimised Priors and Visual Tracking

Global communications rely on subsea cable infrastructure that remains vulnerable to damage from natural hazards and human activity. Autonomous underwater vehicles (AUVs) offer an efficient means to inspect long sections of exposed cable, but uncertainty in cable route maps, small cable diameters and partial burial makes continuous tracking a challenge. This paper presents a novel cable search and tracking method that leverages uncertain prior cable route maps. Graph-based optimisation continuously update the cable route to remain consistent with visual observations. Route uncertainty is constrained as a function of distance from observations using physics-based catenary models that account for cable parameters (i.e., lay depth, diameter, and density), bounding the search space to physically feasible regions and improving search efficiency. Cable detection is performed using a semi-supervised classifier running in real-time on-board a camera-equipped AUV. These detections both update the graph-based optimisation and enable visual cable tracking. When tracking is lost due to misclassification, burial or imperfect control, the bounded search space enables efficient recovery. The approach was demonstrated in field trials using the University of Southampton's Smarty200 AUV. The system successfully located the cable despite deliberate errors in it initial cable route map, updating this to be consistent with observations and using visual tracking to inspect up to 59% of a 120m test cable, with successful recovered after tracking loss.

A Review on Plastic Artificial Neural Networks: Exploring the Intersection between Neural Architecture Search and Continual Learning

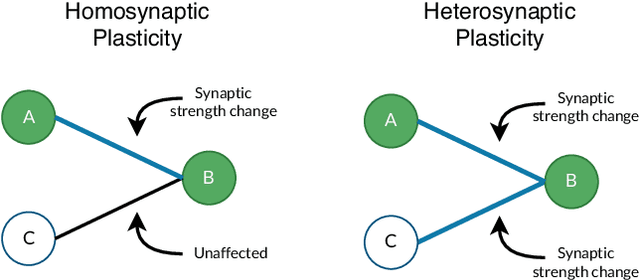
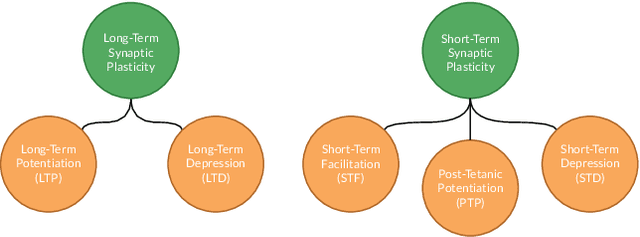
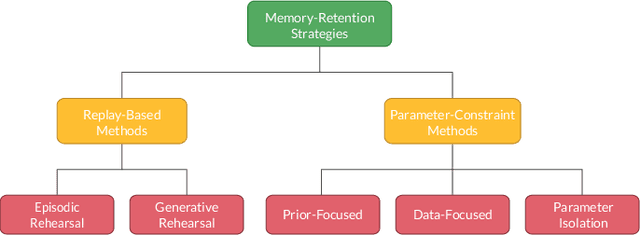
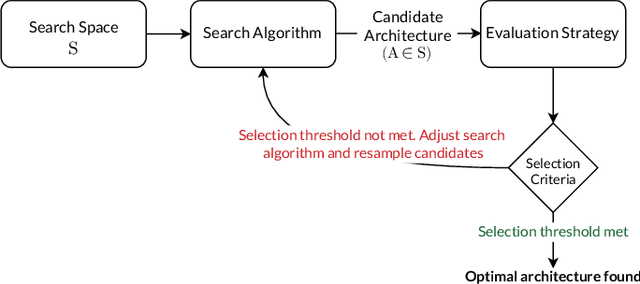
Despite the significant advances achieved in Artificial Neural Networks (ANNs), their design process remains notoriously tedious, depending primarily on intuition, experience and trial-and-error. This human-dependent process is often time-consuming and prone to errors. Furthermore, the models are generally bound to their training contexts, with no considerations of changes to their surrounding environments. Continual adaptability and automation of neural networks is of paramount importance to several domains where model accessibility is limited after deployment (e.g IoT devices, self-driving vehicles, etc). Additionally, even accessible models require frequent maintenance post-deployment to overcome issues such as Concept/Data Drift, which can be cumbersome and restrictive. The current state of the art on adaptive ANNs is still a premature area of research; nevertheless, Neural Architecture Search (NAS), a form of AutoML, and Continual Learning (CL) have recently gained an increasing momentum in the Deep Learning research field, aiming to provide more robust and adaptive ANN development frameworks. This study is the first extensive review on the intersection between AutoML and CL, outlining research directions for the different methods that can facilitate full automation and lifelong plasticity in ANNs.

An Overview of Schema Theory

The purpose of this paper is to give an introduction to the field of Schema Theory written by a mathematician and for mathematicians. In particular, we endeavor to to highlight areas of the field which might be of interest to a mathematician, to point out some related open problems, and to suggest some large-scale projects. Schema theory seeks to give a theoretical justification for the efficacy of the field of genetic algorithms, so readers who have studied genetic algorithms stand to gain the most from this paper. However, nothing beyond basic probability theory is assumed of the reader, and for this reason we write in a fairly informal style. Because the mathematics behind the theorems in schema theory is relatively elementary, we focus more on the motivation and philosophy. Many of these results have been proven elsewhere, so this paper is designed to serve a primarily expository role. We attempt to cast known results in a new light, which makes the suggested future directions natural. This involves devoting a substantial amount of time to the history of the field. We hope that this exposition will entice some mathematicians to do research in this area, that it will serve as a road map for researchers new to the field, and that it will help explain how schema theory developed. Furthermore, we hope that the results collected in this document will serve as a useful reference. Finally, as far as the author knows, the questions raised in the final section are new.