Precision at the indistinguishability threshold: a method for evaluating classification algorithms

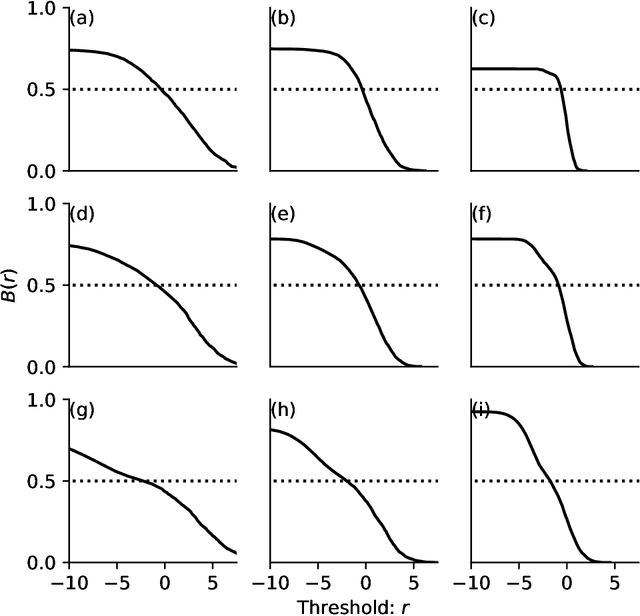
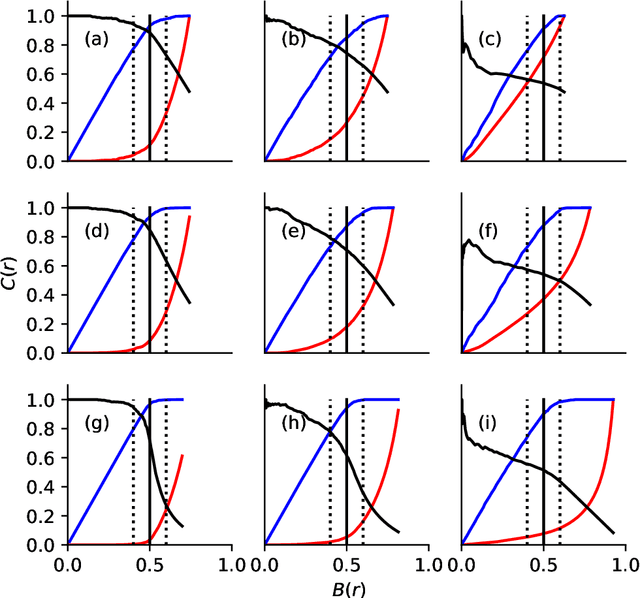
There exist a wide range of single number metrics for assessing performance of classification algorithms, including AUC and the F1-score (Wikipedia lists 17 such metrics, with 27 different names). In this article, I propose a new metric to answer the following question: when an algorithm is tuned so that it can no longer distinguish labelled cats from real cats, how often does a randomly chosen image that has been labelled as containing a cat actually contain a cat? The steps to construct this metric are as follows. First, we set a threshold score such that when the algorithm is shown two randomly-chosen images -- one that has a score greater than the threshold (i.e. a picture labelled as containing a cat) and another from those pictures that really does contain a cat -- the probability that the image with the highest score is the one chosen from the set of real cat images is 50\%. At this decision threshold, the set of positively labelled images are indistinguishable from the set of images which are positive. Then, as a second step, we measure performance by asking how often a randomly chosen picture from those labelled as containing a cat actually contains a cat. This metric can be thought of as {\it precision at the indistinguishability threshold}. While this new metric doesn't address the tradeoff between precision and recall inherent to all such metrics, I do show why this method avoids pitfalls that can occur when using, for example AUC, and it is better motivated than, for example, the F1-score.

The Lost Art of Mathematical Modelling

We provide a critique of mathematical biology in light of rapid developments in modern machine learning. We argue that out of the three modelling activities -- (1) formulating models; (2) analysing models; and (3) fitting or comparing models to data -- inherent to mathematical biology, researchers currently focus too much on activity (2) at the cost of (1). This trend, we propose, can be reversed by realising that any given biological phenomena can be modelled in an infinite number of different ways, through the adoption of an open/pluralistic approach. We explain the open approach using fish locomotion as a case study and illustrate some of the pitfalls -- universalism, creating models of models, etc. -- that hinder mathematical biology. We then ask how we might rediscover a lost art: that of creative mathematical modelling. This article is dedicated to the memory of Edmund Crampin.