Dario Garcia Garcia
On the Regularization of Autoencoders
Oct 21, 2021
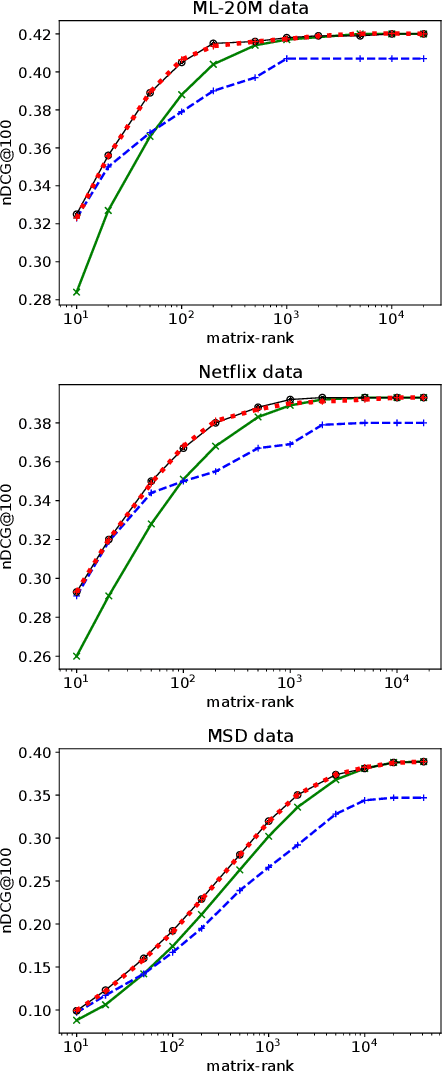
Abstract:While much work has been devoted to understanding the implicit (and explicit) regularization of deep nonlinear networks in the supervised setting, this paper focuses on unsupervised learning, i.e., autoencoders are trained with the objective of reproducing the output from the input. We extend recent results [Jin et al. 2021] on unconstrained linear models and apply them to (1) nonlinear autoencoders and (2) constrained linear autoencoders, obtaining the following two results: first, we show that the unsupervised setting by itself induces strong additional regularization, i.e., a severe reduction in the model-capacity of the learned autoencoder: we derive that a deep nonlinear autoencoder cannot fit the training data more accurately than a linear autoencoder does if both models have the same dimensionality in their last hidden layer (and under a few additional assumptions). Our second contribution is concerned with the low-rank EDLAE model [Steck 2020], which is a linear autoencoder with a constraint on the diagonal of the learned low-rank parameter-matrix for improved generalization: we derive a closed-form approximation to the optimum of its non-convex training-objective, and empirically demonstrate that it is an accurate approximation across all model-ranks in our experiments on three well-known data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge