Decomposing Hard SAT Instances with Metaheuristic Optimization

In the article, within the framework of the Boolean Satisfiability problem (SAT), the problem of estimating the hardness of specific Boolean formulas w.r.t. a specific complete SAT solving algorithm is considered. Based on the well-known Strong Backdoor Set (SBS) concept, we introduce the notion of decomposition hardness (d-hardness). If $B$ is an arbitrary subset of the set of variables occurring in a SAT formula $C$, and $A$ is an arbitrary complete SAT solver , then the d-hardness expresses an estimate of the hardness of $C$ w.r.t. $A$ and $B$. We show that the d-hardness of $C$ w.r.t. a particular $B$ can be expressed in terms of the expected value of a special random variable associated with $A$, $B$, and $C$. For its computational evaluation, algorithms based on the Monte Carlo method can be used. The problem of finding $B$ with the minimum value of d-hardness is formulated as an optimization problem for a pseudo-Boolean function whose values are calculated as a result of a probabilistic experiment. To minimize this function, we use evolutionary algorithms. In the experimental part, we demonstrate the applicability of the concept of d-hardness and the methods of its estimation to solving hard unsatisfiable SAT instances.

Estimating the hardness of SAT encodings for Logical Equivalence Checking of Boolean circuits

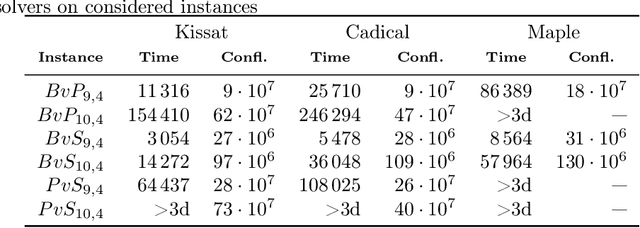
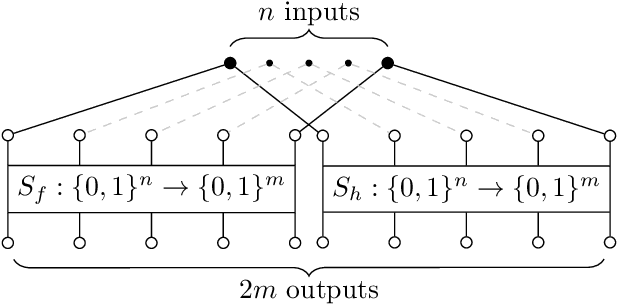
In this paper we investigate how to estimate the hardness of Boolean satisfiability (SAT) encodings for the Logical Equivalence Checking problem (LEC). Meaningful estimates of hardness are important in cases when a conventional SAT solver cannot solve a SAT instance in a reasonable time. We show that the hardness of SAT encodings for LEC instances can be estimated \textit{w.r.t.} some SAT partitioning. We also demonstrate the dependence of the accuracy of the resulting estimates on the probabilistic characteristics of a specially defined random variable associated with the considered partitioning. The paper proposes several methods for constructing partitionings, which, when used in practice, allow one to estimate the hardness of SAT encodings for LEC with good accuracy. In the experimental part we propose a class of scalable LEC tests that give extremely complex instances with a relatively small input size $n$ of the considered circuits. For example, for $n = 40$, none of the state-of-the-art SAT solvers can cope with the considered tests in a reasonable time. However, these tests can be solved in parallel using the proposed partitioning methods.