Estimation in the Gaussian Multiplex Channel

An abstraction for multisensor communication termed the Gaussian Multiplex Channel is presented and analyzed. In this model, the sensor outputs can be added together in any combination through a network of switches, and the combinations can be changed arbitrarily during the observation interval. The sensor output sums are observed in additive Gaussian noise. Using a mean square error cost function and a constraint on the total observation time, an optimal set of combinations (switch positions) and observation times is determined. The solution exhibits high complexity (number of different combinations) even for moderate numbers of sensors. It is then shown that there exists an alternative solution based on Hadamard designs, which achieves the same minimizing MSE cost function and only requires a number of combinations equal to the number of sensors.

Heuristic Sensing Schemes for Four-Target Detection in Time-Constrained Vector Poisson and Gaussian Channels

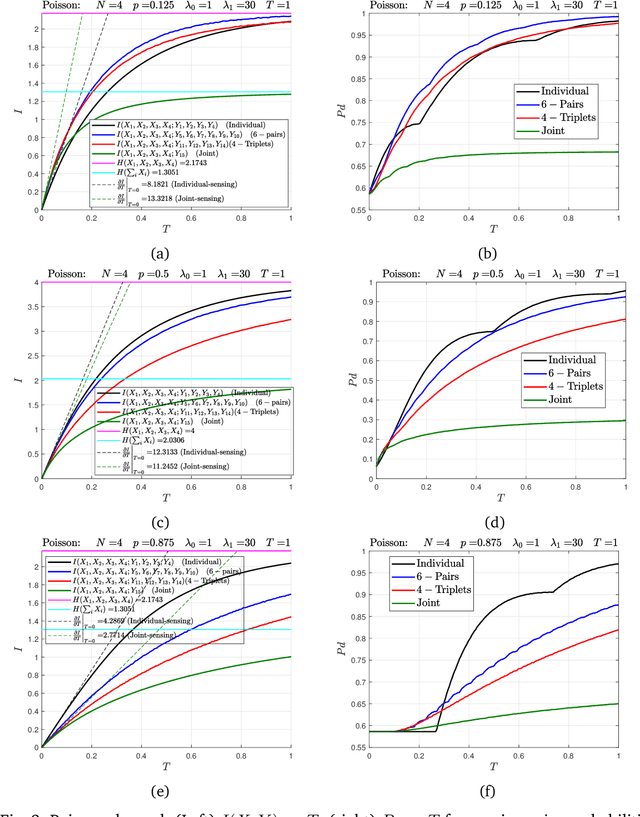
In this work, we investigate the different sensing schemes for the detection of four targets as observed through a vector Poisson and Gaussian channels when the sensing time resource is limited and the source signals can be observed through a variety of sum combinations during that fixed time. For this purpose, we can maximize the mutual information or the detection probability with respect to the time allocated to different sum combinations, for a given total fixed time. It is observed that for both Poisson and Gaussian channels; mutual information and Bayes risk with $0-1$ cost are not necessarily consistent with each other. Concavity of mutual information between input and output, for certain sensing schemes, in Poisson channel and Gaussian channel is shown to be concave w.r.t given times as linear time constraint is imposed. No optimal sensing scheme for any of the two channels is investigated in this work.

Sensing Method for Two-Target Detection in Time-Constrained Vector Gaussian Channel

This paper considers a vector Gaussian channel of fixed identity covariance matrix and binary input signalling as the mean of it. A linear transformation is performed on the vector input signal. The objective is to find the optimal scaling matrix, under the total time constraint, that would: i) maximize the mutual information between the input and output random vectors, ii) maximize the MAP detection. It was found that the two metrics lead to different optimal solutions for our experimental design problem. We have used the Monte Carlo method for our computational work.

Sensing Method for Two-Target Detection in Time-Constrained Vector Poisson Channel

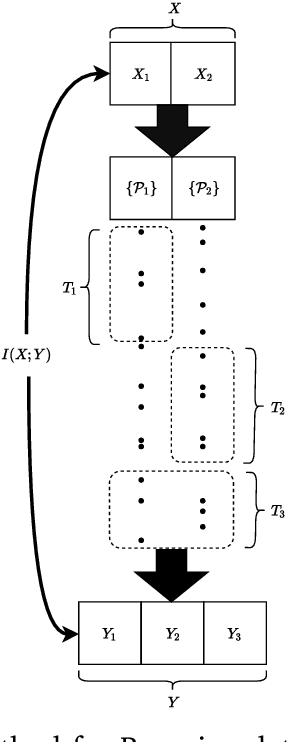
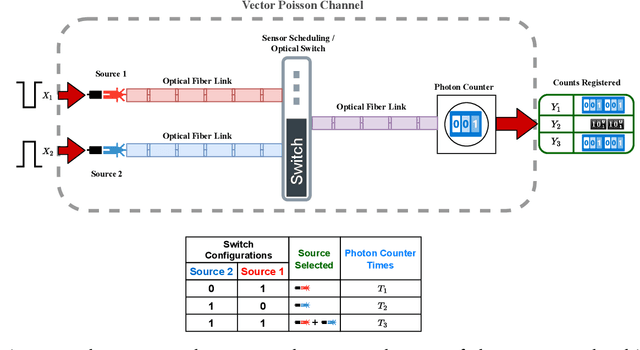
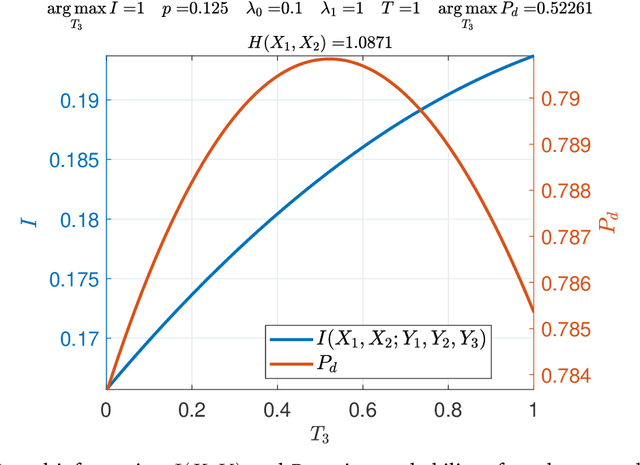
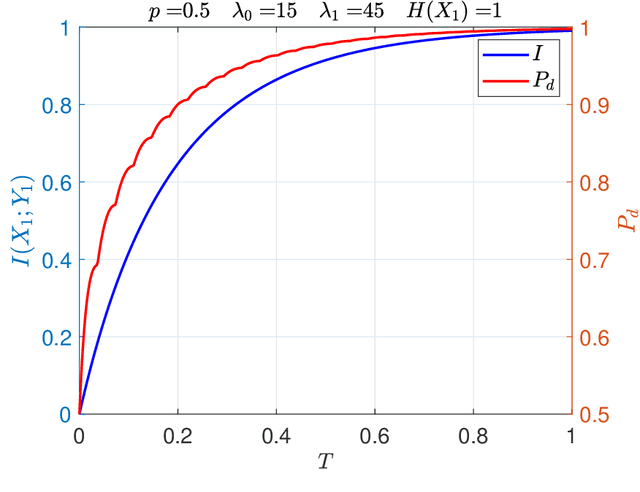
It is an experimental design problem in which there are two Poisson sources with two possible and known rates, and one counter. Through a switch, the counter can observe the sources individually or the counts can be combined so that the counter observes the sum of the two. The sensor scheduling problem is to determine an optimal proportion of the available time to be allocated toward individual and joint sensing, under a total time constraint. Two different metrics are used for optimization: mutual information between the sources and the observed counts, and probability of detection for the associated source detection problem. Our results, which are primarily computational, indicate similar but not identical results under the two cost functions.